不確かさを残さない寸法測定方法はあるのか：製図を極める！ 幾何公差徹底攻略（3）（2/2 ページ）

丸い形状の断面が真円かどうかを判定したい場合、あなたならどうする？ とにかく測定個所を増やしていけば何とかなりそう？

[山田学 ラブノーツ／六自由度技術士事務所，MONOist]

測定の不確かさ

　同じ部位を測定する場合、測定するたびに測定値が変化します。精度とは、「測定結果の正確さと精密さを含めた測定量の真の値との一致の度合い」と定義されます。「測定の不確かさ」とは、「合理的に測定量へ結び付けられ得る値のばらつきを特徴づけるパラメータ」と「JIS Z 8103:2000（計測用語）」で定義されています。

　測定が不確かになる要因には次のようなものがあり、測定結果に影響を与えます。

• What（何を測定するか）：測定対象物の表面のうねり、表面粗さ、傷、重力による変形、基準面の形体など
• When、Where（いつ、どこで測定するか）：器差、温湿度、照明などの熱環境、ほこりや振動、電源ノイズなど
• Who（誰が測定するか）：測定者の測定熟練度、評価計画の知識、測定センスなど
• How（どのように測定するか）：どの測定器を用いて、どのように測定し、何回測るのかなど

　ISO9000により、測定器を使用・管理する上で定期的な校正が求められています。校正とは、例えば理論的に正しい10mmの長さに対して、測定器での計測結果が10mmの許容される規格内にあり、さらに20mm、30mmと連続して切れ目なく測定距離が変化しても、許容される規格内であることを確認する行為をいいます。

　それでは、校正された精密な測定器を用いれば、その部品の大きさと形状がきちんと正確に測定できるのでしょうか？

不確かさが残る測定

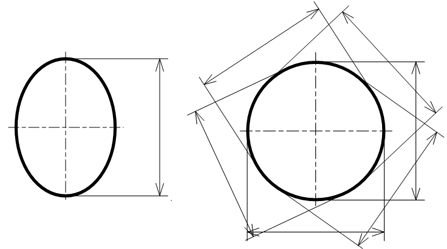
　例えば、ノギスで円筒の直径と真円度を測定したい場合、ノギスで直径の2点間距離を測定します（図8）。ところが、1カ所だけの測定では、真円に近い形状であるとは限らず、楕円である可能性も否定できません。つまり、「測定の不確かさ」が残ります。

図8　不確かさが残る測定：左図は不確かさを残した測定、右図は不確かさを残さないように何回か測定を試みるが……

　ノギスで測定する点を、2点あるいは3点と測定ポイントを増やせば増やすほど、測定の精度が上がります。そこで、何点かを測定して、それらの2点間距離の結果がまったく同じ数値であれば、真円度ゼロ（理論的に正しいゆがみのない円形）といえるのでしょうか？

不確かさが残らない測定って？

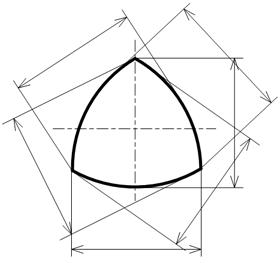
　実は、円筒形状の直径である2点間距離を満遍なく測定したところで、真円かどうかの判断はできないのです。なぜなら、「ルーローの三角形」（おにぎり形の三角）のような、定幅図形と呼ばれる形状であれば、どこを測定しても真円と同じように同じ直径寸法を示すからです（図9）。

図9　直径が同じでも真円とは限らない例

機械製図　虎の巻：「定幅図形」

　図形を平行線で挟んだとき、図形をどの向きに回しても、平行線の幅が一定になる図形のことをいいます。定幅図形は円だけではなく、ルーローの三角形（右図）などがあります。定幅図形は、「マンホールの蓋」などに使われ、どの方向の幅も同じため、誤って蓋を中に落としてしまうことがありません。ロータリーエンジンに使用されるローターは、ルーローの三角形の形状を持ち、まゆ形のシリンダー内で偏芯回転運動を行います。

寸法測定に基準はどこ？

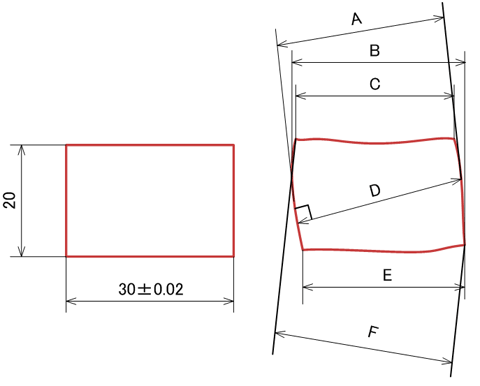
　下図に示す部品図を描き、加工後の部品を計測してみます。ところが、部品は加工熱や工具摩耗などの影響により、面はうねり、角度は90度からわずかに狂ったものができ上がります。カタチが崩れた部品の横幅「30±0.02」の寸法を測定する場合、皆さんはA〜Fのどの測定結果が正解だと思いますか？（図10）

図10　左は図面の寸法指示、右は現物の寸法測定

　実は、寸法は“2点間の距離”を計測するため、どの測定結果でも正解だといわざるを得ないのです。

　CAD上では水平、垂直のX-Y座標が決まっており、真横に線を描くとその線は“水平という概念”を持ちます。ところが、加工バラツキによってカタチが崩れた部品では、水平、垂直という基準がどれか分かりません。空中に浮かせてノギスやマイクロメーターで2点間の距離を測っても、定盤の上で測ってもよいため、寸法公差に入るように計測もできるし、部品不良になるように計測もできてしまいます。

　よって、測定の不確かさという以前の問題で、測る人の解釈によっても、測定結果が大きく異なることになります。

　そこで、計測方法まで指示ができる幾何公差図面が必要となるのです。幾何公差を正しく指示した図面では、寸法解釈に一義性を持たせることができ、誰が測定しても同じ基準で同様の計測方法で測定が可能となるのです。ただし、前述の“測定の不確かさ”は残るため、測定者の意思でバラツキが発生しないよう注意しなければいけません。

　幾何公差を使った図面で製作した部品は、定盤の上でハイトゲージやダイヤルゲージを用いて測定されます。自由曲面など複雑な形状の場合は、3次元測定機を使います。以降の回の解説にも、時々出てきますのでよく覚えておいてください。

---

　次回は、幾何公差の基準を意味するデータムについて解説します。「データムを制するものが幾何公差を制する」といっても過言ではない大変重要なファクターです。（次回に続く）

Profile

山田 学（やまだ まなぶ）

1963年生まれ。ラブノーツ代表取締役、技術士（機械部門）。カヤバ工業（現、KYB）自動車技術研究所で電動パワーステアリングの研究開発、グローリー工業（現、グローリー）設計部で銀行向け紙幣処理機の設計などに従事。兵庫県技能検定委員として技能検定（機械プラント製図）の検定試験運営、指導、採点にも携わる。2006年4月、技術者教育専門の六自由度技術士事務所を設立。2007年1月、ラブノーツを設立し、会社法人（株式会社）として技術者教育を行っている。著書に『図面って、どない描くねん！』『読んで調べる 設計製図リストブック』（共に日刊工業新聞社刊）など。

◎併せて読みたい「CAD」関連ホワイトペーパー：

» 主要7製品を完全網羅！　製品選定・比較に役立つ「商用3D CADカタログ 完全版」

» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”

» 設計現場の56.5％が3D CADを活用、2次元からの「移行予定なし」も16.7％

» エクスペリエンス時代に向けて進化を続ける「CATIA」

» PTCが語る3D CADの歴史と「Creo」の注目機能

⇒ CAD関連の新着ホワイトペーパーはこちら