【問題18】 カルノー図によるカウンタ回路の設計：完全マスター！ 電子回路ドリル II（20）

今回は、クロック信号によってすべてのD-FFが同時に動く“クロック同期カウンタ”の作成について詳しく解説します！

[横田一弘 埼玉県立新座総合技術高等学校 教諭，＠IT MONOist]

【問題17】の解答

　前回の宿題【問題17】は、「すべてのD-FFがクロックに同期している3ビットカウンタを作成する」という問題でした。

　皆さん解けましたでしょうか？

　解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。

　それでは、解答を発表します！

問題17

答え．

【問題17】の解説

　【問題17】は、「クロック信号によってすべてのD-FFが同時に動く」、すなわち“クロック同期カウンタ”を作成する問題です。

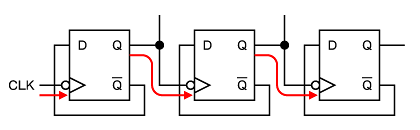
　図1のようにD-FFを順次接続したカウンタでは、前のけたのD-FFの出力により次のけたのD-FFが動作する構成になっているため、上位のけたのD-FFの動作が遅れてしまいます。これでは高速に動作するような回路や複雑に入り組んだ回路を実現することが難しいため、LSIの設計などでは使われていません。

図1　非同期カウンタ回路の信号の伝搬

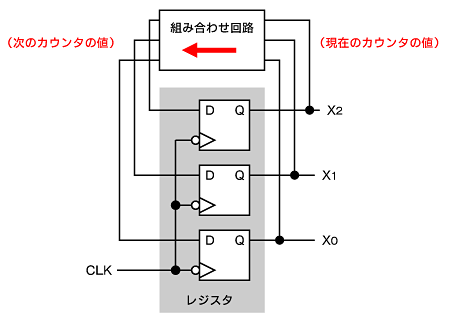
　そこで、すべてのフリップフロップがクロック信号によって同時に動作する、同期カウンタを考えてみます。

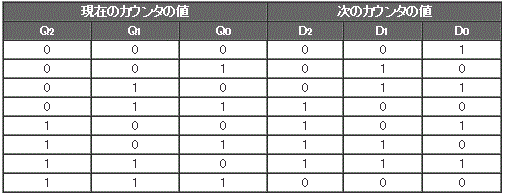
　図2のようにすべてのD-FFにクロックを直接接続します。すると、D-FFはクロックに同期して入力を保持します。組み合わせ回路により、“次のカウンタの値（表1）をバックすれば、クロックごとにカウントされた値がD-FFに保持される”という仕組みです

図2　3ビット同期カウンタの構成

表1　3ビット同期カウンタの真理値表

　それでは、表1から論理回路を作ってみましょう。

　真理値表から回路を作る方法は【問題7】の解説で紹介しました。結果が“1”となる組み合わせに注目して、次のように論理式を求めます。

D0 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0

D1 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0

D2 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0

　続いて、上記の論理式を変形して簡単化します。やり方は、【問題9】の解説を参考にしてください。

D0 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0　
　　＝ （ Q1 ＋ Q1 ） ・ Q2 ・ Q0 ＋ （ Q1 ＋ Q1 ） ・ Q2 ・ Q0　
　　＝ （ Q2 ＋ Q2 ） ・ Q0　
　　＝ Q0

D1 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0　
　　＝ （ Q2 ＋ Q2 ） ・ Q1 ・ Q0 ＋ （ Q2 ＋ Q2 ） ・ Q1 ・ Q0　
　　＝ Q1 ・ Q0 ＋ Q1 ・ Q0

D2 ＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ・ Q0　
　　＝ Q2 ・ Q1 ・ Q0 ＋ （ Q0 ＋ Q0 ） ・ Q2 ・ Q1 ＋ （ Q1 ＋ Q1 ） ・ Q2 ・ Q0　
　　＝ Q2 ・ Q1 ・ Q0 ＋ Q2 ・ Q1 ＋ Q2 ・ Q0

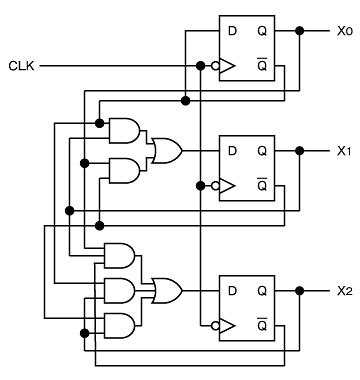
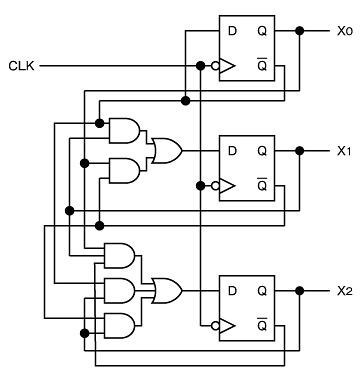
　これらを論理回路で表すと図3のようになります。

図3　3ビット同期カウンタの回路

　以上のような手法を用いることで、「組み合わせ回路」の設計から「順序回路」を作ることができます。

次回までの宿題 ― 【問題18】

問題18

【問題17】の解法を基に、3ビット同期ダウンカウンタを作ってください

答え． 解答はこちら（←クリック）