【問題9】 ゲート回路の簡単化：完全マスター！ 電子回路ドリル II（9）

真理値表から論理式を導く方法を用いて、ビットを加算する最も基本的な加算器である「半加算器（Half Adder）」の回路を作成します。

[横田一弘 埼玉県立新座総合技術高等学校 教諭，＠IT MONOist]

【問題8】の解答

　前回の宿題【問題8】は、真理値表を基に2進数の1けたを加算する回路を作る問題でした。

　皆さん解けましたでしょうか？

　解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。

　それでは、解答を発表します！

問題8

答え．

【問題8】の解説

　【問題8】はビットを加算する最も基本的な加算器、すなわち半加算器（Half Adder）を作る問題です。

　今回も【問題7】の解説で説明した真理値表から論理式を導く方法を用いて、【問題8】のデジタル回路を作成していきます。

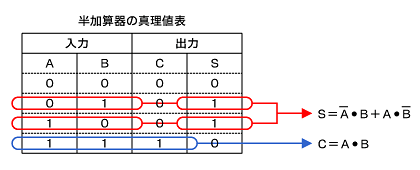
　図1のようにAとBの和S（sum）と、けた上がりC（carry）が“1”になるところに注目して、

S ＝ A ・ B ＋ A ・ B

C ＝ A ・ B

と論理式を求めます。

図1　半加算器の真理値表と論理式

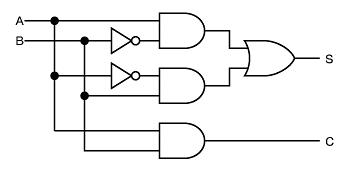
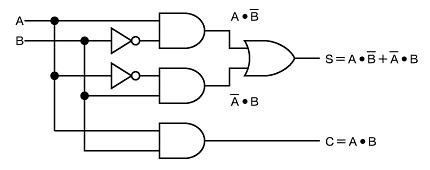
　そして、この論理式を回路で表現すると図2のようになります。

図2　半加算器の回路

　以上でビットの加算回路が完成しました。

　では、nビットの加算回路はどのように作ると思いますか？

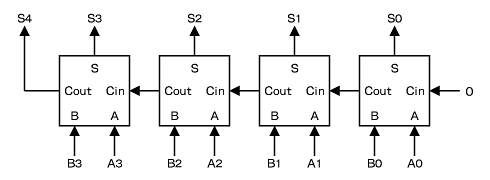
　図3をご覧ください。【問題2】の解説のとおり、2進数の加算では“けた上げ（carry）”を考慮する必要があります。そこで図3の加算回路では、下のけたからのキャリー入力Cinと、上のけたへのキャリー出力Coutを持った全加算器（Full Adder）を使っています。

図3　4ビット加算回路の構成

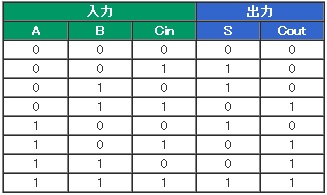
　この全加算器の論理式は、表1の真理値表から、

表1　全加算器の真理値表

S ＝ A ・ B ・ Cin ＋ A ・ B ・ Cin ＋ A ・ B ・ Cin ＋ A ・ B ・ Cin

Cout ＝ A ・ B ・ Cin ＋ A ・ B ・ Cin ＋ A ・ B ・ Cin ＋ A ・ B ・ Cin

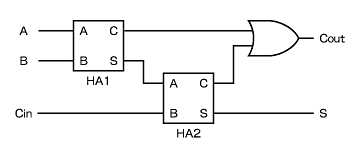
と求められます。ここから導き出されるゲート回路は少し複雑なものになりますが、図4のように2つの半加算器HAを組み合わせて作ることができます。

図4　全加算器の回路

次回までの宿題 ― 【問題9】

問題9

次の真理値表のように、3つの入力A、B、Cのうち2つ以上“1”が入力されたとき、出力Xが“1”となる「多数決回路」をできるだけ少ないゲートで作ってください

答え． 解答はこちら（←クリック）