【問題3】 負の数の2進表現：完全マスター！ 電子回路ドリル II（3）

今回は、2進数の「加算」「減算」「乗算」を行ううえで、ポイントとなる“けた上げ”“けた借り”などについて詳しく解説します。

[横田一弘 埼玉県立新座総合技術高等学校 教諭，＠IT MONOist]

【問題2】の解答

　前回の宿題【問題2】は、2進数の加算・減算・乗算の問題でした。皆さん解けましたでしょうか？

　解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。

　それでは、解答を発表します！

問題2

1. （1011）₂ ＋ （110）₂ ＝ 答え．（10001）₂
2. （1011）₂ − （110）₂ ＝ 答え．（101）₂
3. （1011）₂ × （110）₂ ＝ 答え．（1000010）₂

【問題2】の解説

2進数の加算

　それでは、「（1011）₂ ＋ （110）₂ ＝ ？」の求め方について解説します。

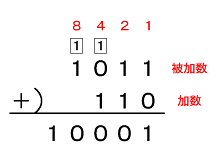
　図1を見てください。2進数の加算は10進数の場合と同様に下のけたから計算を行います。

図1　2進数の加算

　まず、1のけたは1 ＋ 0 ＝ 「1」となります。

　次に、2のけたは1 ＋ 1 ＝ 「2」。つまり、（10）₂となります。従って、“けた上げ（carry）”が生じ、2のけたは「0」となります。

　続いて、4のけたを計算します。ここでは、先ほどのけた上げを含めて加算します。つまり、1 ＋ 0 ＋ 1 ＝ 2 ＝ （10）₂です。さらに、ここでもけた上げが生じ、4のけたは「0」となります。

　最後に、8のけたを計算します。先ほどのけた上げがあるので1 ＋ 1 ＝ 2 ＝ （10）₂となり、答えは「（10001）₂」と求められます。

2進数の減算

　続いて、「（1011）₂ − （110）₂ ＝ ？」の求め方について解説します。

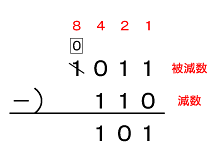
　図2を見てください。2進数の減算も10進数の場合と同様に下のけたから計算を行います。

図2　2進数の減算

　まず、1のけたは1 − 0 ＝ 「1」となります。

　次に、2のけたは1 − 1 ＝ 「0」となります。

　続いて、4のけたを計算します。この場合、0から1を引くことができないので、8のけたから“けた借り（borrow）”をします。従って、8のけたの被減数は「0」となり、4のけたは2 − 1 ＝ 「1」となります。よって答えは「（101）₂」と求められます。

2進数の乗算

　最後に、「（1011）₂ × （110）₂ ＝ ？」の求め方について解説します。

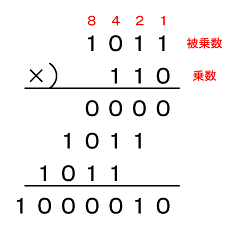
　図3を見てください。2進数の乗算は、10進数での乗算方法と同様に行います。

図3　2進数の乗算

　まず、被乗数を1のけたの乗数で掛けます。乗数の1のけたは0なので、その値は（0000）₂となります（この場合、（0000）₂なので省略しても構いません）。

　次に、被乗数を2のけたの乗数で掛けます。乗数の2のけたは1なので、その値は（1011）₂ですが、10進数の場合と同じように1けたずらしておきます。

　続いて、被乗数を4のけたの乗数で掛けます。ここでも乗数は1なので、被乗数をさらに1けたずらしておきます。

　最後に、これらを足し合わせ「（1000010）₂」と求められます。

次回までの宿題 ― 【問題3】

問題3

「−5」を2進数で表すと？ 8ビットの2の補数で表してください

答え． 解答はこちら（←クリック）