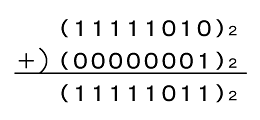【問題4】 符号付き2進数と符号なし2進数：完全マスター！ 電子回路ドリル II（4）

「high」と「low」のいわゆる“ビットデータ”で表現されるデジタル回路の世界で、負の数をどのように扱えばよいのでしょうか？

[横田一弘 埼玉県立新座総合技術高等学校 教諭，＠IT MONOist]

【問題3】の解答

　前回の宿題【問題3】は、“負の数の2進表現”に関する問題でした。皆さん解けましたでしょうか？

　解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。

　それでは、解答を発表します！

問題3

「−5」を2進数で表すと？ 8ビットの2の補数で表してください。

答え．（11111011）₂

【問題3】の解説

　【問題3】は2進数で負の数をどのように取り扱うかという問題です。

　われわれが負の数を扱うとき、−5のように「−（マイナス記号）」を数の前に付けて表します。しかし、デジタル回路では、H（high）とL（low）のいわゆるビットデータしか扱うことができません。

　ここで負の数のビット表現を考えてみましょう。

　「ある負の数と対応する正の数の和は“ゼロ”」です。従って−5では、

5 ＋ （ −5 ） ＝ 0

という式が成り立ちます。

　これを基に、−5の2進数（ビット表現）を考えると、

（ 101 ）₂ ＋ （ x ）₂ ＝ 0

となり、「x」の部分が−5に相当します。

　以上を踏まえたうえで、詳しい解説に入りますが、先に【問題3】の答えを明かします。

　答えは「（11111011）₂」です。

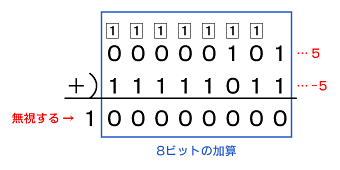
　では、この答えで本当に「5 ＋ （ −5 ） ＝ 0」が成立するかどうかを確認してみましょう。

　図1の計算式を見ると、最上位にけた上がりが生じますが、続く8ビットはゼロになり「5 ＋ （ −5 ） ＝ 0」の計算が成り立ちます。

図1　8ビットがゼロになることを確認

　以上のような負の数の表現方法を「2の補数表現」といい、2の補数は2進数の加減算に適合することからコンピュータの世界でよく使われます。

　それではここで、2の補数の求め方について解説します。

　最初に対応する正の数を2進数に変換します。−5の場合、5を2進数に変換します。これを8ビットで表現すると、

5 ＝ （00000101）₂

となります。

　次に、各ビットの「0」を「1」に、「1」を「0」に反転させます。すると

（11111010）₂

となります。

　最後に、これに「1」（つまり「（00000001）₂」）を加えれば終了です（図2）。

図2　2の補数の求め方

　図2から−5は「（11111011）2」と求められます。

次回までの宿題 ― 【問題4】

問題4

8ビットの2進数で表現できる数の最大値と最小値はいくつですか？ また16ビット、32ビットではそれぞれいくつですか？

答え． 解答はこちら（←クリック）