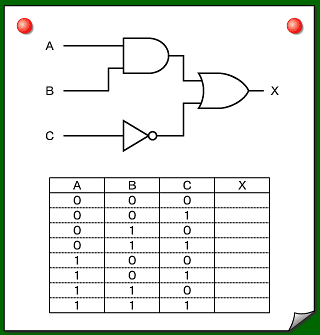
【問題5】 組み合わせ論理回路：完全マスター！ 電子回路ドリル II（5）

今回は、負の数を扱わない絶対値表現「符号なし2進数」と2の補数で負の数を扱う「符号付き2進数」について詳しく解説します。

[横田一弘 埼玉県立新座総合技術高等学校 教諭，＠IT MONOist]

【問題4】の解答

　前回の宿題【問題4】は、決められたビット数で表現できる数の最大値と最小値を求める問題でした。皆さん解けましたでしょうか？

　解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。

　それでは、解答を発表します！

問題4

8ビットの2進数で表現できる数の最大値と最小値は？

答え．最大値 255　最小値 −128

16ビットでは？

答え．最大値 65535　最小値 −32768

32ビットでは？

答え．最大値 4294967295　最小値 −2147483648

【問題4】の解説

　【問題3】では、ビットデータで負の数を表現する方法、すなわち“2の補数”を紹介しました。

　しかし、2の補数について、まだ次のような疑問があります。

　例えば、−5は2の補数で、

• 8ビットで、（11111011）₂
• 16ビットで、（1111111111111011）₂

などと表しますが、これは単なるビットデータなので、

（11111011）₂は、251

（1111111111111011）₂は、65531

と区別できません。

　そこで、コンピュータの世界では「数を表すビット数」と「負の数の扱い」をあらかじめ決めておくのです。

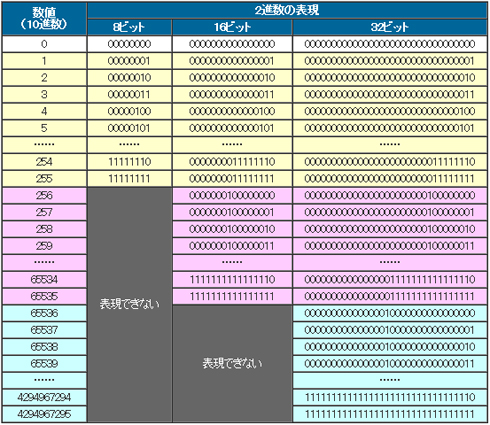
符号なし2進数

　「符号なし2進数」は、負の数を扱わない絶対値表現をいいます。

　nビットの符号なし2進数では、「0」から「2のn乗 − 1」までの数を表します。つまり、表1のように、

• 8ビットでは、「0」から「2の8乗 − 1 ＝ 255」まで
• 16ビットでは、「0」から「2の16乗 − 1 ＝ 65535」まで
• 32ビットでは、「0」から「2の32乗 − 1 ＝ 4294967295」まで

が表現できる数の範囲となります。

表1　「符号なし2進数」で表現できる数

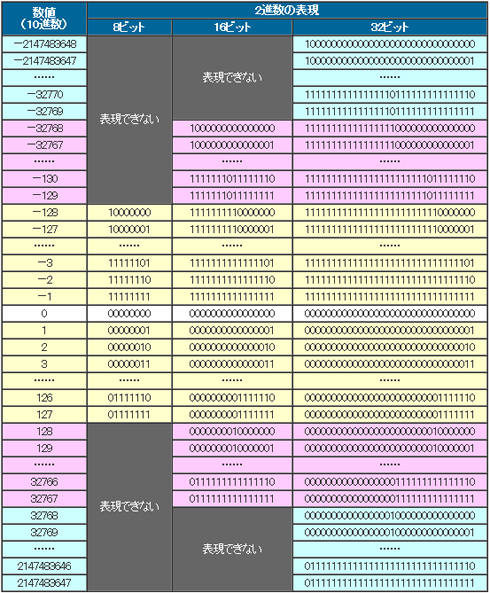
符号付き2進数

　「符号付き2進数」は、2の補数で負の数を扱います。

　表2のように、最上位ビット（左端のビット）が0のときはゼロまたは正の数、1のときは負の数であると決められています。

　nビットの符号付き2進数では、「−2のn−1乗」から「2のn−1乗 − 1」までの数を表します。つまり、

• 8ビットでは、「−2の7乗 ＝ −128」から「2の7乗 − 1 ＝ 127」まで
• 16ビットでは、「−2の15乗 ＝ −32768」から「2の15乗 − 1 ＝ 32767」まで
• 32ビットでは「−2の31乗 ＝ −2147483648」から「2の31乗 − 1 ＝ 2147483647」まで

が表現できる数の範囲となります。

表2　「符号付き2進数」で表現できる数

　もう【問題4】の答えはお分かりですね。

　最大値は符号なし2進数で、

• 8ビットで「255」
• 16ビットで「65535」
• 32ビットで「4294967295」

となります。

　最小値は符号付き2進数で、

• 8ビットで「−128」
• 16ビットで「−32768」
• 32ビットで「−2147483648」

となります。

次回までの宿題 ― 【問題5】

問題5

次の論理回路の真理値表を完成させてください

答え． 解答はこちら（←クリック）