【問題2】 2進数の加減算と乗算:完全マスター! 電子回路ドリル II(2)
日常生活で使用している“10進数”とコンピュータの世界で使われる“2進数”を相互に変換する「基数変換」の方法を解説します。
【問題1】の解答
前回の宿題【問題1】は、“電子回路で数をどのように扱うのか”を問うもので、10進数と2進数を相互に変換する問題でした。皆さん解けましたでしょうか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けてください。
それでは、解答を発表します!
問題1
2進数の「 10110 」を10進数で表すと?
答え:22
10進数の「 25 」を2進数で表すと?
答え:11001
【問題1】の解説
まず、10進数(decimal number)と2進数(binary number)について解説します。
10進数とは、
- 「0」「1」「2」「3」「4」「5」「6」「7」「8」「9」の10種類の数字で表す
- 基数(radix)が10である
という数を表す方法で、われわれが日常生活で使っているものです。
また、基数とは“けた上がりの基準となる数”のことです。10進数の場合、1(10の0乗 )の位、10(10の1乗)の位、100(10の2乗)の位、1000(10の3乗)の位、……のように、1つけたが上がるごとにけたの重さが10倍になっていきます。
そして、2進数は、
- 「0」「1」の2種類の数字で表す
- 基数が2である
という数を表す方法で、コンピュータの世界で使われるものです。電子回路においても2進数の「0」と「1」が、デジタル回路の「L(low)」と「H(high)」に対応するため、2進数が使われています。
2進数の場合、1(2の0乗)の位、2(2の1乗)の位、4(2の2乗)の位、8(2の3乗)の位、16(2の4乗)の位、……のように、1つけたが上がるごとにけたの重さが2倍になっていきます。
本連載では、10進数と2進数を区別するために、2進数を「(10110)2」のように表します。ちなみに、左から「イチ ゼロ イチ イチ ゼロ」と1字ずつ読みます。
それでは、【問題1】を解いていきましょう。
まずは、「2進数の『(10110)2』を10進数で表すと?」からです。
図1を見てください。これは、(10110)2の“けたの重み”を記したものです。
そして、以下のように数字が1であるけたの重みを足し合わせることで、2進数を10進数に変換することができます。
16 + 4 + 2 = 22
よって答えは、「22」と求められます。
次に、「10進数の『25』を2進数で表すと?」を解いてみましょう。
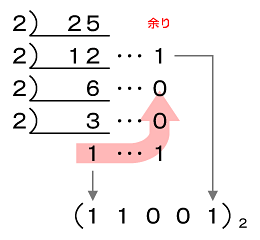
図2のように商が1になるまで「25」を2で割っていき、その余りを最後の数字から順に並べることで、10進数を2進数に変換することができます。
よって答えは、「(11001)2」と求められます。
次回までの宿題 ― 【問題2】
問題2
以下の2進数の計算をしてください
- (1011)2 + (110)2 = ?
- (1011)2 − (110)2 = ?
- (1011)2 × (110)2 = ?
答え. 解答はこちら(←クリック)
Copyright © ITmedia, Inc. All Rights Reserved.