冷却系の設計を自分でやってみる企画を総括する:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(19)(1/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第19回では、本連載のこれまでの内容を総括する。また、記事後半では「ベルヌーイの式」について取り上げる。
本シリーズは「ストップ! 外注丸投げ」と銘打ち、CAE解析とExcelを使いながら冷却系の設計を自分でできるようになりたい設計者に向けた連載です。
ところで、「外注丸投げ」は本当に悪なのでしょうか。限られた社内リソースで自社開発を進めている間に、ライバル企業が社外リソースをうまく活用し、新しいモノやサービスをいち早く提供してしまうこともあります。不得意な分野は、それを得意とする企業に任せ、自社は得意分野で強みを最大限発揮すれば、双方が専門性を生かせるため、迅速かつ低コストで、質の高い開発が進むでしょう。
しかし、ここでいう「外注」はそうした前向きな活用を指しているわけではありません。例えば、生産ラインが何らかの理由で停止したり、客先の機械に不具合が発生したりした際に、設計を丸投げした外注設計者に指示を仰ぐだけ、あるいは部品の図面番号を確認するためだけに電話をかける――こうした“依存的な状況”を指しています。
筆者がある工場で仕事をしていたときのことです。夜の8時ごろ、誰かが外注さんに「まだ帰らないでくださいね」と電話している場面に遭遇しました。このように外注への依存度が高すぎると、問題の解決に時間がかかったり、余計なコストが発生したりして、さまざまな弊害が生じます。
これは少し極端な例かもしれませんが、自分自身で設計していれば、前述のような事態には陥らないと考えています。では、このシリーズの総括をしていきましょう。
設計のスタイル
本シリーズを執筆する際、前提としていた設計のスタイルは以下のようなものでした。このスタイルを実践するために必要な事項について、これまで解説してきたつもりです。なお、シミュレーションの一部、あるいは全てを実験で代替することも十分にあり得ます。
- 設計対象の重要なパラメーターを予測する計算式を導出する
- 上記の計算を行うExcelシートを作成する
- 1〜2ケースでシミュレーションを実施し、その結果と計算結果を比較して計算精度を確認する。同時にシミュレーションモデルを改善し、シミュレーション精度を高める
- 設計パラメーターをさまざまに変化させ、設計制約を満足する解を求める
- もう少し欲を出すなら、パフォーマンスをコストで割った値(いわゆるコスパ)が最も良くなるパラメーターの組み合わせを求めて設計を行う
- 最終設計案のシミュレーションを行う
本来であれば、V&V(Verification & Validation)といって、シミュレーション精度の妥当性を確認するために理論解を用います。しかし、本シリーズでは「紙と鉛筆による計算」の誤りをチェックするために、シミュレーションを活用してきました。逆の使い方でしたね。
前述した設計手順の延長として、製品や機械の開発においては、次のような流れが考えられます。
- 開発対象の挙動を記述できる解析モデルを構築する。この段階で、多くの項目をパラメーター化しておくと、後の作業が楽になる
- 解析モデルを計算できる環境を整える。これは「シミュレーター」と呼ぶことができ、Excelシートの場合もあれば、CAE解析の場合もある
- パラメーターサーベイ(parametric study)を行い、最適解を求める
- 最適解の妥当性を、シミュレーションや実験によって確認する
- 4.の作業で期待した結果が得られない場合は、解析モデルに立ち返り、モデルを修正して最適解を再度求める
- 開発対象の詳細設計、試作、評価試験を行う
これらの手順は筆者の我流ではありますが、まずは「シミュレーター」を作ることがポイントです。Excelシートは規模こそ小さいものの、立派なシミュレーターと呼んで差し支えないと考えています。
熱伝導と熱伝達
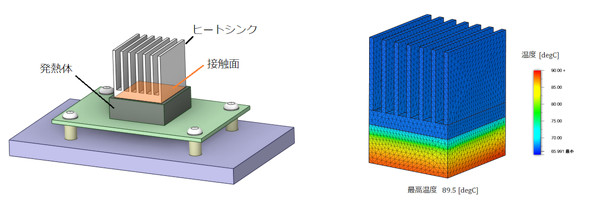
ヒートシンクと電線を題材に、熱伝導および熱伝達の計算方法とシミュレーション事例を紹介しました。前者はデカルト座標系(xyz直交座標系)、後者は円筒座標系でした。図1にヒートシンクとその温度分布を示します。
図1右図は温度分布を示したもので、ヒートシンクの色は青一色であり、内部に温度差は見られません。ヒートシンクはアルミニウム合金製で熱伝導率が高く、冷却に適した材料です。つまり、以下のような関係が成り立ちます。
熱伝導率が高い → 温度勾配がほとんどない → 温度差がない
熱伝導率について覚えておいてほしいポイントがあります。それは、アルミ押出材の熱伝導率が134[W/m.K]であるのに対し、オーステナイト系ステンレス鋼(SUS304など)は15[W/m.K]と、およそ10分の1であるという点です。つまり、ステンレス鋼でヒートシンクを作ると冷却性能は約10分の1となり、冷却を目的とする部品には適しません。
また、金属材料の場合、熱伝導率と電気の導電率が比例関係にあるため、ステンレス鋼の電気抵抗はアルミのおよそ10倍になります。
さらに、ステンレス鋼は一見すると錆びていないように見えますが、表面には「不動態膜」と呼ばれるクロムの酸化膜が形成されており、この膜は絶縁性を持ちます。ステンレス鋼にテスターを当てると電気抵抗は測定できますが、なぜ電気が流れるのかはやや複雑な話です。基本的には、表面に絶縁膜があると考えた方がよく、電気を通す用途の部品には使わない方が無難です。
ここで「ちょっと待った」といって紹介したのが接触熱抵抗です。固体表面はどれだけ滑らかに仕上げても微細な凹凸があり、実際に接触している面積は見掛けの面積よりも桁違いに小さくなります。フーリエの法則から、熱の移動量は面積に比例するため、固体同士の接触面では熱伝導効率が低下します。
図1の温度分布を見ると、発熱体内部の温度は連続的に変化していますが、ヒートシンクとの接触面では、発熱体が水色、ヒートシンクが青色となり、温度差が生じています。つまり、温度分布に不連続が見られます。このような場合は、熱伝導グリスを使用することで熱抵抗を低減できます。
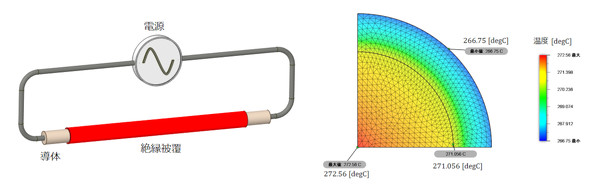
次に、絶縁被覆された銅線の温度分布を紹介しました。円筒座標系で温度分布を計算していたところ、原稿執筆中に「円筒座標系の半径にはマイナス値が存在しない」という事実に気付きました。半径座標がマイナスになる世界はなく、そこに熱は伝わりません。
そのため、r=0[m]における熱流束はゼロとなります。これは温度勾配もゼロであることを意味し、温度分布グラフの傾きがr=0の位置で水平になることを示します。この関係は積分定数を求める際の境界条件として利用できます。
筆者が若いころ、コイルの設計をしていたとき、導体に流せる電流は断面積に比例するものだと思い込んでいました。しかし、電線便覧を見てそうではないことに気付きました。このことを紹介したいと考え、銅線を題材に取り上げたのでした。
Copyright © ITmedia, Inc. All Rights Reserved.