公差計算の代表的な2つの考え方と使い分け：若手エンジニアのための機械設計入門（6）（2/2 ページ）

3D CADが使えるからといって、必ずしも正しい設計ができるわけではない。正しく設計するには、アナログ的な知識が不可欠だ。連載「若手エンジニアのための機械設計入門」では入門者が押さえておくべき基礎知識を解説する。第6回は、公差計算の代表的な2つの考え方と、その使い分けについて取り上げる。

[土橋美博／スワニー，MONOist]

総厚から部品の公差を求める

　では、アセンブリ全体に与えられたサイズ公差から、構成部品それぞれのサイズ公差を求めると、どのようになるのでしょうか。

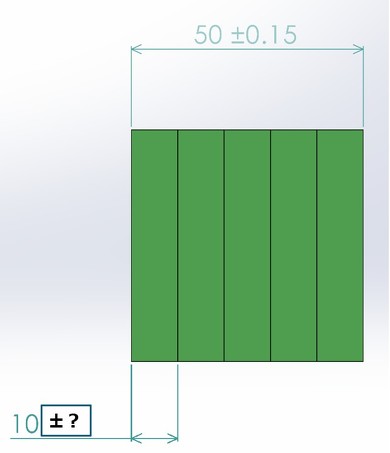
　例えば、アセンブリの総厚が50mmで、そのサイズ公差をJIS B 0405-1991の「精級」に準じて±0.15mmとしたい場合を考えます。このとき、共通仕様の5枚の部品の板厚にどのようなサイズ公差を設定すればよいかを、互換性の方法と不完全互換性の方法のそれぞれの観点から見ていきます。

図3　総厚50±0.15mmのアセンブリから部品の図示寸法とサイズ公差を算出［クリックで拡大］

1．互換性の方法による計算式

• 部品公差：T₁＋T₁＋T₁＋T₁＋T₁＝0.15　→T₁＝0.03
• 部品の図示寸法と公差：10±0.03

2．不完全互換性の方法による計算式

• 部品公差：√T₂²＋T₂²＋T₂²＋T₂²＋T₂²＝0.15　→T₂≒0.067
• 部品の図示寸法と公差：10±0.067

　このように比較すると、不完全互換性の方法で求めた部品公差は、互換性の方法で求めた値よりも約√5倍、大きな許容範囲となっていることが分かります。

　つまり、アセンブリの総厚を必ず50±0.15mmに収めたい場合には、互換性の方法に基づく厳しい部品公差（±0.03mm）を適用する必要があります。一方、多少の確率的なバラつき（外れ値）が発生することを許容できる場合には、不完全互換性の方法により、より緩やかな部品公差（±0.067mm）を適用することが可能となります。

製品の目的に応じた設計判断がカギ

　公差の考え方一つで、製品の精度、品質、コストは大きく変化します。ここでは、互換性の方法と不完全互換性の方法について、それぞれの特徴とどのように使い分けるべきかについて説明します。

1．互換性の方法

• 特徴：
  • 全ての部品が公差範囲の最大ズレで組み合わされることを前提とした設計手法
  • どの部品とでも確実に組み立てできる完全な互換性が保証される
  • 安全側での設計となるため、公差値への要求が厳しくなる
• メリット：
  • 組み立て精度が常に保証される
  • 部品を自由に交換できる
• デメリット：
  • 精度が厳しくなる分、加工の難易度が上がり製造コストが高くなりやすい

2．不完全互換性の方法

• 特徴：
  • 部品の寸法バラつきは正規分布に従うという統計的な考え方に基づく
  • 全ての部品が最大ズレに偏ることはほとんどなく、中心値付近に収まることを前提とする
  • 統計的に不良品が発生する可能性を許容する設計前提である
• メリット：
  • 部品の公差を緩く設定できる
  • 製造コストを抑えられ、歩留まりが向上する
  • 量産に適している
• デメリット：
  • 完全な互換性がないため、部品交換時に組み立て誤差が発生するリスクがある
  • 統計的品質管理が必要となる
  • 部品寸法のバラつきが正規分布していないと正確な評価が困難である

3．使い分けの考え方（筆者の見解）

• 互換性の方法は安全かつ確実な公差設計であり、交換性が求められる製品に最適である
• 不完全互換性の方法は現実的かつ効率的な公差設計であり、コストを重視する量産に有効である。なお、検査を行うことで許容値を外れた製品の検出が可能である
• 公差設計においては、製品の目的や使用環境、生産方式に応じて適切な方法を選択することが重要である

---

　次回は、公差計算の具体的な手順や算出方法について解説します。お楽しみに！　（次回へ続く）

Q&Aで学ぶこの記事のポイント

Q1. なぜ公差設計が重要なのですか？

A. 部品などを製造する際、「人・機械・材料・方法（4M）」の要因によって、どうしても寸法にバラつきが生じます。そのため、製品の機能や品質を安定させるには、こうしたバラつきを前提に「どの程度までズレを許容できるか」をあらかじめ設計段階で定める必要があります。それが「公差設計」です。

Q2. 「互換性の方法」とは何ですか？

A. 「互換性の方法」は、各部品の寸法が最悪のケース（ワーストケース）でズレた場合を想定し、全ての部品が組み合わさっても機能を果たせるよう設計する手法です。この方法では、どの部品を交換しても組み立て寸法が必ず許容範囲内に収まり、完全な互換性が確保されます。ただし、部品の公差が厳しくなるため、製造コストは高くなります。

Q3. 「不完全互換性の方法」とは何ですか？

A. 「不完全互換性の方法」は、部品の寸法が正規分布に従うという統計的な前提の下、全ての部品が最大ズレになる確率は低いと考えて公差を緩く設定する手法です。この方法では製造コストが抑えられ、量産向きですが、完全な互換性は保証されません。

Q4. どちらの公差計算を使うべきですか？

A. 目的や製品の使用条件などによって使い分ける必要があります。

　使い分けのイメージ：

• 互換性の方法は部品の交換性や高い信頼性が求められる製品に向いています
• 不完全互換性の方法はコストや歩留まり重視の量産製品に適しています

　公差設計は、設計者の判断力が試される重要なポイントです。

⇒ 連載バックナンバーはこちら

著者プロフィール

土橋美博（どばし よしひろ）

半導体組み立て関連装置メーカー、液晶パネル製造関連装置メーカーを経て、「メイドINジャパンを、再定義する。」有限会社スワニーに入社。CIOとして最新デジタルツールによるデジタルプロセスエンジニアリング推進に参画する。

ソリッドワークス・ジャパンユーザーグループ（SWJUG）、ワールドワイドのソリッドワークス・ユーザーグループネットワーク（SWUGN）のリーダーも務める。