データムを必要とする幾何公差【その1】〜姿勢公差の平行度〜：産機設計者が解説「公差計算・公差解析」（8）（1/4 ページ）

機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第8回はデータムを必要とする幾何公差をテーマに、姿勢公差の平行度について取り上げる。

[土橋美博／飯沼ゲージ製作所，MONOist]

　ここまで、「データム（Datum）」を必要としない幾何公差について取り上げてきました。今回からは“データムを必要とする幾何公差”をテーマに解説を進めていきます。

　あらためて、データムとは何か？　ですが、「JIS B 0022:1984 幾何公差のためのデータム − Datums and datum-systems for geometrical tolerances」を確認すると、

関連形体に幾何公差を指示するときに、その公差域を規制するために設定した理論的に正確な幾何学的基準

と定義されています。詳しい内容については、連載第4回「『データム』とは何か？　をあらためて理解する」で説明しているのでぜひご覧ください。

表1　※機械要素JIS要覧（新日本法規出版）を参考に作成

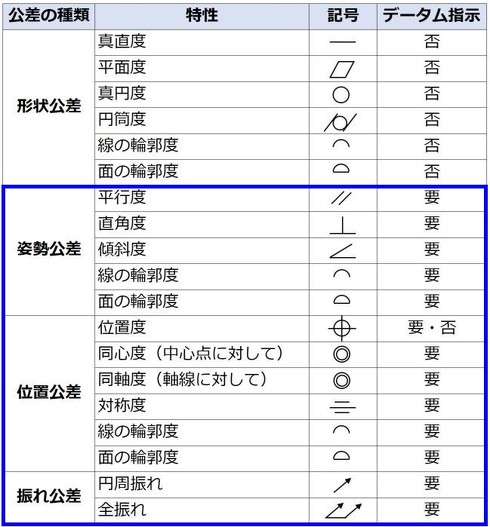
　データムを必要とする幾何公差には、表1の青色枠で示した通り、大きな分類として「姿勢公差」「位置公差」「振れ公差」があります。これらは「真円度」「平面度」といった、他の線や面に関係せず、ある理想的な形状に対して単独でその許容範囲となる公差を指示するものとは異なり、“関連形体の幾何公差”となります。

1．姿勢公差（attitude tolerance）

　姿勢公差は、対象となる形体がデータムと関連し、平行、直角、任意の角度を持つ幾何学的に正しい姿勢を表す偏差が許容値内にあるかを規定します。幾何公差において、データムを参照することから「関連形体」と呼ばれています。なお、前回まで説明してきた“データムを参照しない幾何公差”を「単独形体」と呼びます。

　姿勢公差には、以下に示す5つの幾何公差があります。

1. 平行度（Parallelism）
2. 直角度（Perpendicularity）
3. 傾斜度（Angularity）
4. 線の輪郭度（Profile of a Line）
5. 面の輪郭度（Profile of a Surface）

　それでは、順を追って説明していきます。

1−1．平行度（Parallelism）

　まず、平行度ですが「JIS B 0621:1984 幾何偏差の定義及び表示」（以下、JISとします）によると、

データム直線、データム平面に対して平行な幾何学的直線または幾何学的平面からの平行であるべき直線形体または平面形体の狂いの大きさ

と定義されています。

　平面といってもその面は凸凹しています。その凸凹の最も高い部分と最も低い部分が、上下に離れた2つの平面の間に挟まれた一定距離［mm］の中にあることを定義します。データムが不要な平面度と異なるのは、その2つの平面を規定するための基準面がデータムとして存在する点です（平面度は形状公差となります）。

　平行度には、以下の種類（用途）があります（「JIS B 0621:1984 幾何偏差の定義及び表示. Definitions and designations of geometrical deviations」参照［以下、JIS B 0621］と記載）。

1. 直線形体のデータム直線に対する平行度
2. 直線形体または平面形体のデータム平面に対する平行度
3. 平面形体のデータム直線に対する平行度