確率統計で考える公差設計：若手エンジニアのための機械設計入門（7）（1/2 ページ）

3D CADが使えるからといって、必ずしも正しい設計ができるとは限らない。正しく設計するには、アナログ的な知識が不可欠だ。連載「若手エンジニアのための機械設計入門」では、入門者が押さえておくべき基礎知識を解説する。第7回では、設計におけるバラつきを前提に、確率統計の考え方を公差設計にどう応用するかを分かりやすく説明する。

[土橋美博／スワニー，MONOist]

　連載「若手エンジニアのための機械設計入門」では、機械設計を始めて間もない若手エンジニアの皆さんを対象に、機械設計で知っておくべき基礎知識や考え方などについて解説していきます。

　前回は、公差計算の基本的な考え方である「互換性の方法」と「不完全互換性の方法」について、交換性が求められる製品やコスト重視の量産製品への適用といった観点から、製品の目的や使用環境、生産方式に応じて、適切な方法を選択できることを解説しました。

　部品を組み合わせて製品を作る際、設計図に記載の寸法通りにモノができるわけではありません。どんなに高精度な加工機を使っても、寸法には必ず“バラつき”が生じます。これは、加工条件や機械の状態、材料特性など、さまざまな要因が重なって発生する自然な現象です。だからこそ、設計者はそのバラつきを見越して、寸法に「公差（許容範囲）」を設定する必要があります。しかし、ここで難しいのは「どこまで許してよいのか」という判断です。

　公差を厳しくすれば、加工精度は上がりますが、コストが跳ね上がります。逆に、公差を緩くすればコストは下がりますが、製品の機能や組み立てがうまくいかなくなる恐れがあります。このバランスをどう見極めるかが、公差設計の核心であり、設計者の力量が問われるポイントです。このように、機械設計において公差は非常に重要な要素となります。

確率統計的な考え方

　では、どうやってその「ちょうどよい公差を見つけるのか？」――そこに必要となってくるのが、「確率」や「統計」の考え方です。互換性の方法と不完全互換性の方法について、確率統計的な視点からあらためて説明します。

互換性の方法

　「どんな部品の組み合わせでも、必ず確実に組み立てられるようにしよう」という考え方です。例えば、部品Aが最大寸法、部品Bが最小寸法という“最悪の組み合わせ”になっても、きちんと組み立てができるように設計します。つまり、「確率的に100％確実に大丈夫な状態」にしておくというやり方です。安全ではありますが、その分、厳しい公差（＝精度の高い加工）を要求することになるため、製造コストが高くなりがちです。

不完全互換性の方法：統計的公差設計

　「現実のモノづくりでは、最悪な組み合わせはほとんど起きない」という発想に基づく手法です。現場で加工された部品のサイズにはバラつきがあるものの、多くは平均値に近い寸法で仕上がります。これをグラフにすると「山の形（正規分布）」になります。この考え方を用いることで、「全ての部品が公差の端ギリギリになる確率は非常に低い」ことが分かります。そこで、実際に起こる確率に合わせて公差を少し緩めることで、加工しやすくなり、コストも抑えられるという考え方です。

統計の視点がカギになる不完全互換性の方法

　不完全互換性の方法には、確率や統計の考え方が欠かせません。

• 寸法のバラつきを「正規分布」として扱う
• 構成部品の累積公差を「二乗和平方根」で合計する
• 多数の組み合わせをシミュレーションする

といった統計的な手法を用います。

　もちろん、こうした方法で公差解析や設定を行うためには、「加工のバラつき具合」や「加工現場の実績データ」、すなわちサンプルデータが必要です。サンプルデータに基づいて、加工工程における実力値から適切な公差の設定を行う必要があります。設計者が設定しようとしている値が、実力値に対して余裕のある値なのか、それとも実現が難しい値なのかを、正しく見極めなければなりません。

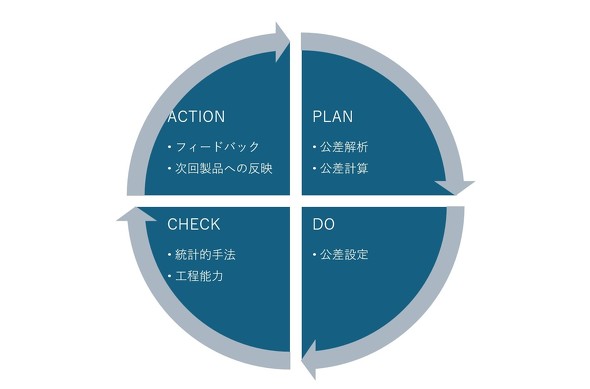
　さらに重要なのは、「設定した公差の結果として、実際に加工されたものがどうであったかを確認し、その結果を設計にフィードバックする」というフローです。これを「公差設計のPDCA」といいます（図1）。

図1　公差設計のPDCA［クリックで拡大］

寸法のバラつきを正規分布として扱う考え方

　「寸法のバラつきを正規分布で扱う」と聞くと、少し難しく感じる方もいるかもしれません。しかし、これは決して特別な理論ではなく、現場で日々発生している“当たり前のこと”を確率統計的に表現したにすぎません。

　例えば、ある軸の直径をΦ10.00mmに加工するとします。図面上では10.00mmと指示されていても、実際に測定してみると、9.99mmや10.01mmといった、わずかにズレた値が含まれることがあります。加工工程に異常がなければ、100本製作した場合、平均値である10.00mmに近い寸法が多く、両端の寸法は少なくなる傾向があります。

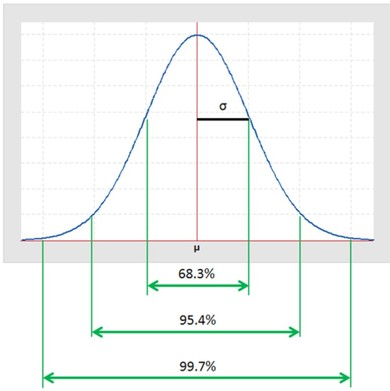
　この「中心に山があり、両側に向かって滑らかに減っていく」グラフの形こそが、正規分布と呼ばれるものです。正規分布の特徴は、「バラつきの幅（＝標準偏差）」さえ分かれば、「その範囲に何％の部品が収まるか」を予測できる点にあります。

　例えば、バラつきの幅が±3σであれば、その範囲内に99.7％の部品が収まります。つまり、0.3％は範囲外となり、分かりやすくいえば「1000個製作すると、そのうち約3個が規格外になる可能性がある」ということです。

　設計者がこの確率統計的な視点をもって不完全互換性の方法を理解していれば、公差を不必要に厳しくすることを避けられます。つまり、現場の実力を信頼しつつ、製品としての成立を統計的に見込むことが可能になります。

確率統計的に公差を考えた例

　ここでは、確率統計の基礎知識として重要なポイントを紹介します。

正規分布

　正規分布では、平均値の周りにデータがどの程度集まっているかを「σ（シグマ）」という単位で表します。このσは、バラつきの大きさ、すなわち標準偏差を意味します。例えば、次のように考えます。

• 平均から±1σの範囲には約68％のデータが入ります
• ±2σの範囲には約95％
• ±3σの範囲にはほとんど全て（約99.7％）
• ±6σになると、ほぼ完全（99.9997％）に全てのデータが収まります

図2　正規分布と確率［クリックで拡大］

　つまり、バラつきが少ない（＝σが小さい）ほど、データは平均値の近くに集中することになります。どのような大きさの値であっても、標準偏差を用いれば、同様に確率を求めることができます。これこそが、正規分布の大きな特徴です。