ヒートシンクを設計しよう!:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(3)(3/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第3回では、「熱伝達」についておさらいし、ヒートシンクの設計に着手する。
ちょっと待った! 何か忘れていないか?
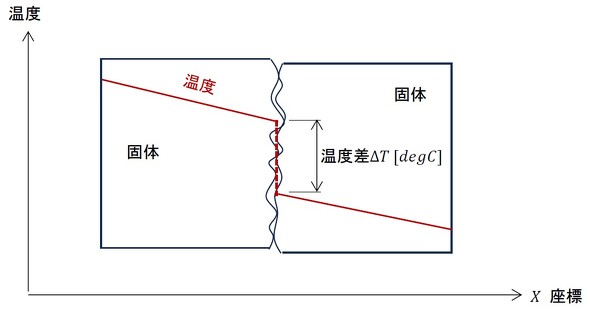
自作PCを製作する際、CPUとヒートシンクの間に熱伝導グリスを塗ります。なぜ必要なのでしょうか。トライボロジーの文献には「真実接触面積」というパラメーターがあります。機械加工部品やCPU表面には「表面粗さ」という凹凸があります。数μmかそれ以下の値ですが、固体同士は凸部だけ接触しています。図7に接触状態の模式図を示します。
熱の流れる方向に向かって温度は下がっていきますが、温度変化は接触面で不連続となります。これは熱が伝わる断面積が接触面で極端に小さくなっているからです。表1のヒートシンク計算シートは「なかなかいい感じ」ではなく、書き換えが必要です。
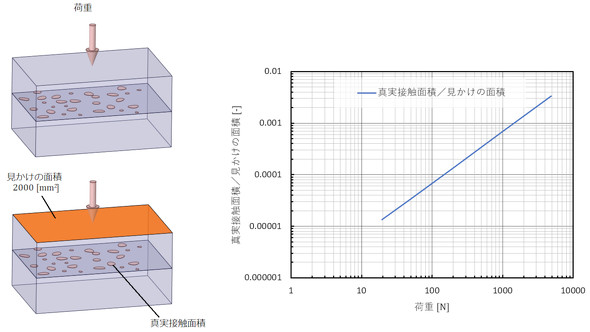
真実接触面積は、見かけの接触面積(縦寸法×横寸法)よりどれくらい小さいのでしょうか。例えば、図8のようになります。真実接触面積は想像を絶するくらい小さいのです。このような事情で図7のような温度の不連続が発生します。
図8に示した通り、荷重が大きいほど真実接触面積が増えます。ということは、ボルトでギューっと締め付けると接触面積が増えて冷却に有利と考えられます。
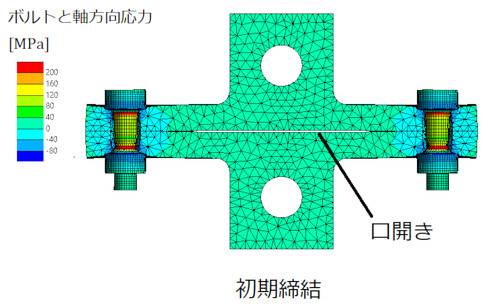
連載「CAEを正しく使い疲労強度計算と有機的につなげる」の第18回「フリーソフトでボルトの疲労破断の有無を予測する」の中で、初期締結状態の接触状態を示しました。これを図9に再掲します。図のように口開きが発生しています。口開きのところの真実接触面積はゼロです。ボルト締結に頼っても接触面積はあまり増えません。
固体同士の接触面の温度差の見積もり
図7の温度差ΔTを求めましょう。伝熱接触抵抗Rというパラメーターを導入します。次式でRを定義します(式7)。Rのことを「接触抵抗」と呼ぶことにします。
接触抵抗の逆数は熱伝達率と同じ次元となり、CAE解析ソフトではこの逆数を入力することが多いです。熱抵抗Rの見積式として「橘・佐野川の式」(参考文献[1])を紹介します。その前に、「ブリネル硬さ(Brinell hardness)」について説明します。
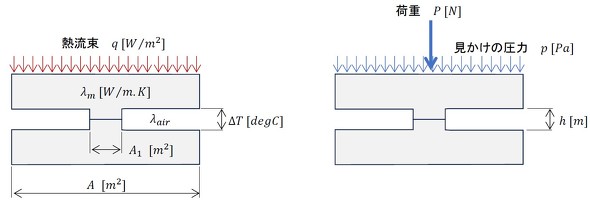
金属の被測定物に超硬合金の球状圧子を一定荷重で押し込むとくぼみができます。くぼみの直径から接触した面積を求め、押し付けた荷重を面積で割ったものがブリネル硬さで、HBWと表記します。荷重/面積なので圧力と同じ次元の量です。熱抵抗を求めるために、図10のような接触面のモデルを考えます。突起のところで固体同士で接触しています。A1が真実接触面積となります。上側の固体が荷重P[N]で押し付けられているとします。
ブリネル硬さは荷重/面積だったので、荷重をブリネル硬さで割った量はつぶれて接触した面積ですね。つぶれて接触した面積は真実接触面積ととても関係があると考えられます。次式を仮定しましょう(式8)。
Cは「とても関係がある」と言った手前、1桁の数です。式8を変形します(式9)。
固体同士が接触しているところの熱流束qmは次式で表されます(式10)。mは“metal”のmです。
接触していないところは空気が充満しており、かつ空気に流れがないとすると、空気の熱伝導による熱流束qairは次式で表されます(式11)。
図10のh寸法は、固体の表面粗さの2倍と考えることができます。フーリエの法則から温度差は次式で表されます(式12)。
真実接触部の温度差は次式で表されます(式13)。式10を代入しておきます。
空気による熱伝導部の温度差は次式で表されます(式14)。ここのhは熱伝達率ではなく、図10に示したギャップの寸法です。
固体同士の接触により移動する熱量Wmと、空気の熱伝導により移動する熱量Wairは、上式から以下となります(式15、式16)。
Copyright © ITmedia, Inc. All Rights Reserved.