フリーソフトでボルトの疲労破断の有無を予測する:CAEを正しく使い疲労強度計算と有機的につなげる(18)(1/6 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第18回では、フリーのFEMソフト「LISA」で疲労破断の有無を予測できないか考える。
本連載も大詰めです。今までボルトの疲労破断の有無の予測に、直交異方性の線膨張率を設定できる有限要素法ソフトか、ボルトプリテンション機能を持つソフトを使ってきました。しかし、このようなソフトは高額です。フリーのFEM(有限要素法)ソフト「LISA」で疲労破断の有無を予測できないか考えてみましょう。
開口するかどうかを判定する位置
前回の内容で得られたヒントは以下となります。
- 開口位置を無理やり決めて、「開口しないこと」を疲労破断しない条件とできないだろうか?
- 開口の有無を固定点の反力で判定できないだろうか?
- 開口の有無を無理やり決めた開口位置近傍の応力で判定できないだろうか?
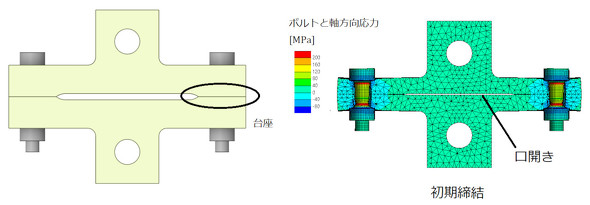
では、開口するかどうかを判断する位置を決めましょう。図1にボルト2本構成の被締結体を示します。前回、開口を検討するために台座を設けました。この台座は強度計算のための台座であって、台座があったからといってボルトの疲労強度は向上しません。鋳物部品なら仕上げ加工のためにこのような形状となりますが、普通は台座なしで設計されます。「強度計算に必要だから台座を付けました」との理由で部品コストの上昇が許されることはないでしょう。というわけで“台座なし”で検討を進めます。
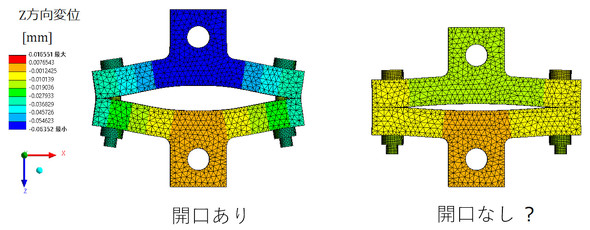
図1右図は初期締結状態です。開口していますが、開口していない領域、言い換えると“口開きから接触に移行する位置”はかなりボルトに近いと推測されます。図2に荷重時の変形図を示します。図2左図は「開口あり」と判断できますが、図2右図については「どのような基準で開口なし」と判断すればよいでしょうか。
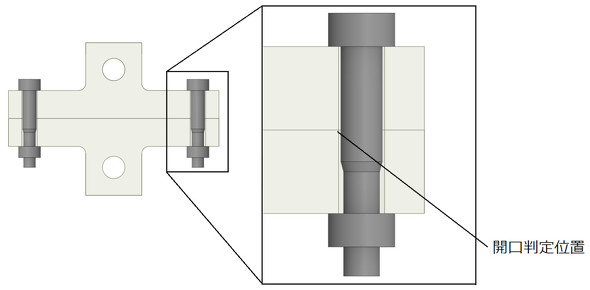
例えば、図3の位置を開口判定位置としてはどうでしょうか。この位置で上側被締結体と下側被締結体が離れていれば「開口あり」、接触していれば「開口なし」と判定するという案です。具体的な方法としては、上側被締結体の開口判定位置の節点変位と下側被締結体の節点変位を読み取って判定します。接触要素を使っているので少し食い込みが発生しますが、そこは目をつぶりましょう。
戦略は以下の通りです。
- 荷重時に開口しなければボルトは疲労破断しないと判断する
「ほんとに大丈夫?」と思われたと推測します。筆者も同じ気分です。では、調べていきましょう。
開口し始める荷重
連載第15回で説明した解析方法を使えば、開口あり/なしが分かりますし、そのときのボルトの応力振幅も分かります。以下の手順で調べることにします。
- 開口ありと開口なしが切り替わるギリギリの荷重を求める
- 上記荷重での応力振幅を求める
- 応力振幅とボルトの疲労強度を比較して安全率を求める
- 安全率が2[-]以上あれば、「荷重時に開口しなければボルトは疲労破断しないと判断する」ことを認める
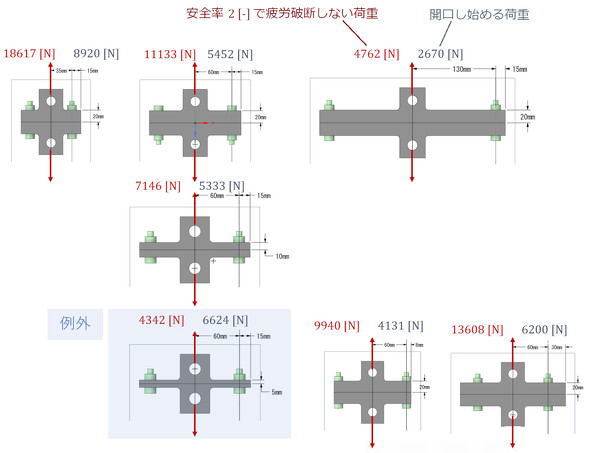
図4に、開口し始める荷重と安全率2[-]で疲労破断しない荷重を示します。
以下に示す式1が成立したら、「荷重時に開口しなければボルト軸部の安全率は2[-]以上あり、ボルトは疲労破断しない」と判断できます。
あらゆるケースで式1が成立したら都合がよいのですが、反例があり式1は常に成立しません。反例を例外扱いとし、図4に記載しました。反例は被締結体が薄いときに出現します。図4の例外のようなバランスの悪い設計は普通しないので、この点に注意すればよいと思います。「例外ありとして、荷重時に開口しなければボルト軸部の安全率は2[-]以上あり、ボルトは疲労破断しない」と判断することにしましょう。
ここでは勝手に安全率を式2として定義していましたね。アンウィンの安全率とは異なります。
Copyright © ITmedia, Inc. All Rights Reserved.