フリーソフトでボルトの疲労破断の有無を予測する：CAEを正しく使い疲労強度計算と有機的につなげる（18）（4/6 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第18回では、フリーのFEMソフト「LISA」で疲労破断の有無を予測できないか考える。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

トポロジー最適化その後

　紙面が余りました。以前お届けした連載「フリーFEMソフトとExcelマクロで形状最適化」の中で「トポロジー最適化」について取り上げました。そこから少し進歩したので簡単にご紹介します。

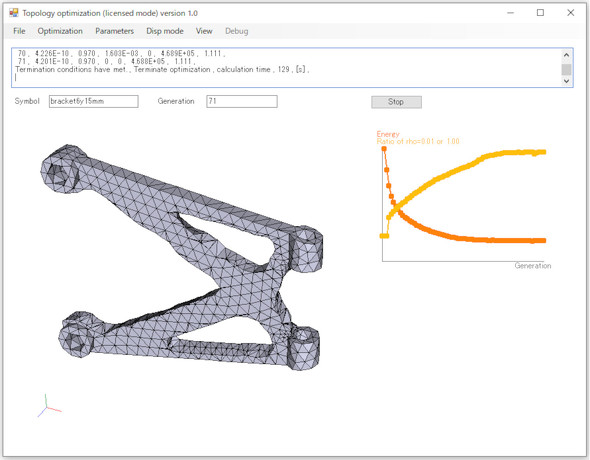
　図15に最適化ソフトの画面を示します。

図15　トポロジー最適化ソフト［クリックで拡大］

　よく見ると、

calculation time , 129 ,［s］

とあります。これくらいなら2分くらいでできるようになりました。

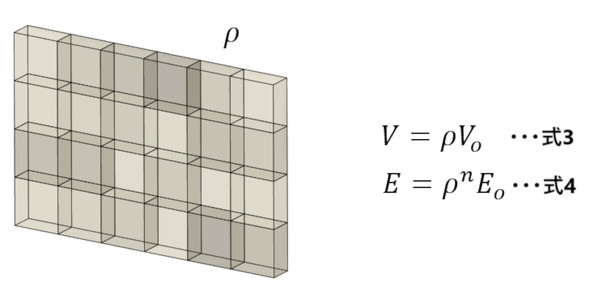
　この最適化は密度法を用いています。図16に要素分割された要素を示します。各要素は“スカスカの軽石のようなもの”とお考えください。各要素は密度ρという属性を持っています。ρ＝1［-］は軽石の中の空間がなくなって軽石ではなく普通の石となった状態です。ρ＝0.01［-］はかなりスカスカな軽石となります。

図16　密度法によるトポロジー最適化の要素［クリックで拡大］

　図16の式3において、Voは軽石の見掛けの体積です。そして、Vは軽石の中の石だけの体積です。ρの定義からρの単位はなくρは無次元量となります。スカスカだったらヤング率も低くなると考えて、式4でヤング率を決めます。Eoは軽石の中の石のヤング率です。鉄鋼材料のトポロジー最適化問題だったら、Eo＝200［GPa］となります。Eは軽石のヤング率です。nは2［-］としました。

　図15のオレンジ色のグラフに注目します。トポロジー最適化では「物体に蓄えられるひずみエネルギー」を目標関数として、目標関数が最小になるように各要素の密度を決めていきます。オレンジ色のグラフはモデル全体に蓄えられるひずみエネルギーの総和で、次式（式5〜7）で計算しています。ひずみエネルギーが最小化されていく様子が分かります。

式5

式6

式7

　図15の黄色のグラフに注目します。トポロジー最適化では密度が1か0にならないと終了できません。黄色のグラフは密度が1か0になっている要素の割合です。これを見て最適化計算の終了を判断します。

　図17に連載「フリーFEMソフトとExcelマクロで形状最適化」で紹介した最適化結果を示します。四角で囲ったところがチェッカーフラグ状態となっていました。

図17　最適化結果：チェッカーフラグ問題［クリックで拡大］

　このチェッカーフラグは計算を進めていくとなくなるわけではなく、残り続けます。このアルゴリズムによるとチェッカーフラグが最適解ということになります。トポロジー最適化は「チェッカーフラグが悪だ」として進化しますが、チェッカーフラグこそが最適解である旨の話をしました。

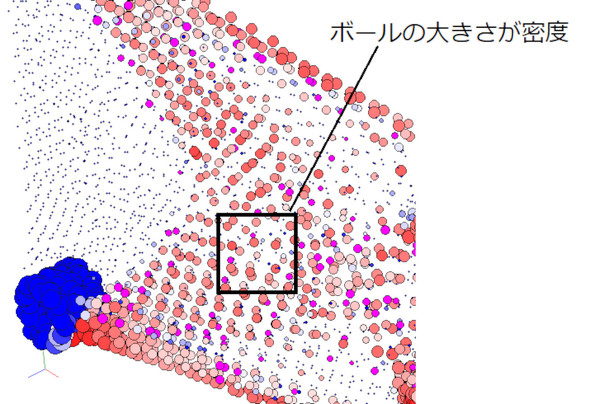
　ここで紹介するトポロジー最適化は3次元問題なので、四面体要素を使います。四面体要素は見た目が三角形なのでチェッカーフラグとならないですが、同様の問題が発生します。図18に四面体要素のチェッカーフラグ問題を示します。ボールの大きさが密度の大きさです。大きなボールの隣に小さなボールがあります。これがチェッカーフラグに相当するものです。

図18　四面体要素のチェッカーフラグ問題［クリックで拡大］

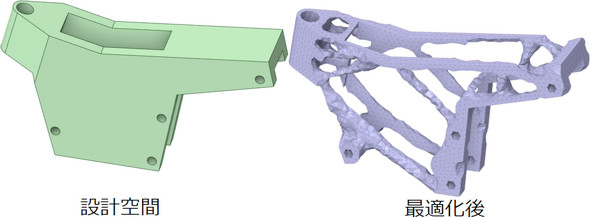
　図18のようにならないように、2つの調整パラメーターを導入しました。このあたりはどこの論文にも書いていないので自身で試行錯誤しました。図19、図20にトポロジー最適化例を示します。

図19　トポロジー最適化事例（1）［クリックで拡大］

図20　トポロジー最適化事例（2）［クリックで拡大］

　図20のように設計空間を限定すると、良い感じのフレームが出来上がります。