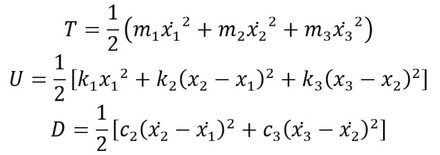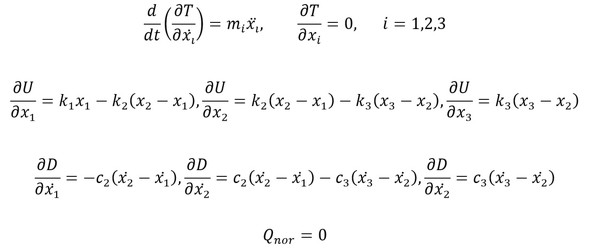連載
ラグランジュの方程式（その2）〜ラグランジュの方程式の導出手順と適用例〜：1Dモデリングの勘所（40）（5/5 ページ）
「1Dモデリング」に関する連載。連載第40回では「ラグランジュの方程式（その2）」と題し、ラグランジュの方程式の導出手順とその結果を具体事例に適用して効果を確認する。さらに、ラグランジュの方程式を粘性減衰がある場合に拡張し、実際の問題に適用してみる。
減衰がある場合のラグランジュの方程式の適用例
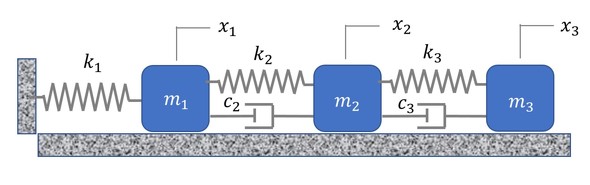
減衰がある場合のラグランジュの方程式の適用例として、図4に示す3自由度系を考える。このとき、マス（質点）は摩擦なく動くものとする。
図4の運動エネルギー、弾性エネルギー、散逸関数は、
となる。これから、
となるので、運動方程式は下記となる。
次回から数回にわたって1Dモデリングの目的、その実現のための基礎や本質について、いま一度原点に立ち返って考えてみたい。 （次回へ続く）
筆者プロフィール：
大富浩一（https://1dcae.jp/profile/）
日本機械学会 設計研究会
本研究会では、“ものづくりをもっと良いものへ”を目指して、種々の活動を行っている。1Dモデリングはその活動の一つである。
- 最新著書：1Dモデリングの方法と事例（日本機械学会）
- 研究会HP：https://1dcae.jp/
- 代表者アドレス：ohtomi@1dcae.jp
Copyright © ITmedia, Inc. All Rights Reserved.
関連記事
1Dモデリングの方法にもさまざまなアプローチがある
「1Dモデリング」に関する連載。連載第4回では、本題である1Dモデリングの方法を取り上げる。まず、1Dモデリングの方法には大きく「モデル生成」「低次元化モデリング」「類推モデリング」の3つのアプローチがあることを説明。特に本稿では1Dモデリング固有の考え方としての類推モデリングについて詳しく解説する。
0Dモデリングとは？ 理論・経験に基づく理論式・経験則が究極の1Dモデリング!?
「1Dモデリング」に関する連載。連載第3回は、理論・経験に基づく理論式・経験則が究極の1Dモデリングであることを、0Dモデリングの定義、3Dモデリングとの関係、幾つかの事例を通して説明する。また、理論・理論式を考えるに当たって重要な“単位”に関して、なぜ単位が必要なのかその経緯も含めて紹介する。
1Dモデリングとは？ モデリングをさまざまな視点から捉えることで考える
「1Dモデリング」に関する連載。連載第2回は、モデリングをその表現方法から2種類の“3つのモデリング”に分けて考える。次に1Dモデリングが必要となる背景について、1DCAEとMBDという2つの製品開発の考え方を紹介し、これらと1Dモデリングの関係を示す。さらに、リバース1DCAEと1DCAEを通して、より具体的に1Dモデリングのイメージを明らかにする。以上を通して、最後に“1Dモデリングとは”について考察する。
モデリングとは何か？ 設計プロセスと製品設計を通して考える
「1Dモデリング」に関する連載。連載第1回は、いきなり1Dモデリングの話に入るのではなく、そもそもモデリングとは何なのか？ について考えることから始めたい。ものづくり（設計）のプロセス、製品そのものを構成する要因を分析することにより、モデリングとは何かを明らかにしていく。
なぜ今デライトデザインなのか？ ものづくりの歴史も振り返りながら考える
「デライトデザイン」について解説する連載。第1回では「なぜ今デライトデザインなのか？」について、ものづくりの変遷を通して考え、これに関する問題提起と、その解決策として“価値づくり”なるものを提案する。この価値を生み出す考え方、手法こそがデライトデザインなのである。
デライトデザインとは？ 3つのデザイン、類似の考え方を通して読み解く
「デライトデザイン」について解説する連載。第2回では、デライトデザインとは？ について考える。まず、設計とデザインの違いについて触れ、ユーザーが製品に期待する3つの品質に基づくデザインの関係性にも言及する。さらにデライトデザインを実行する際に参考となる考え方や手法を紹介するとともに、DfXについて説明し、デライトデザインの実践に欠かせない要件を明確にする。