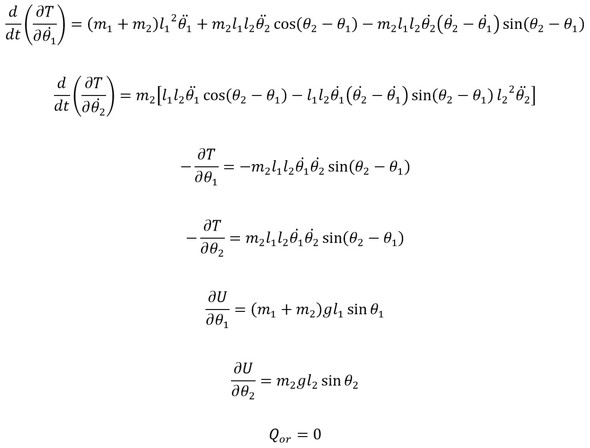ラグランジュの方程式（その2）〜ラグランジュの方程式の導出手順と適用例〜：1Dモデリングの勘所（40）（3/5 ページ）

「1Dモデリング」に関する連載。連載第40回では「ラグランジュの方程式（その2）」と題し、ラグランジュの方程式の導出手順とその結果を具体事例に適用して効果を確認する。さらに、ラグランジュの方程式を粘性減衰がある場合に拡張し、実際の問題に適用してみる。

[大富浩一／日本機械学会 設計研究会，MONOist]

ラグランジュの方程式の適用例

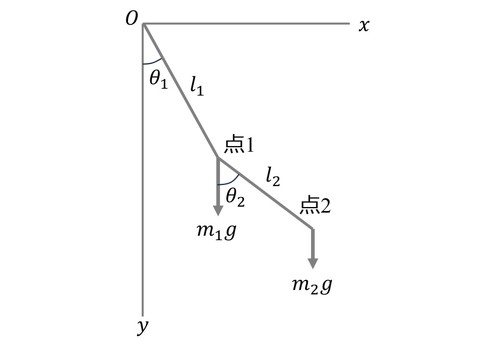
　ラグランジュの方程式の適用例として、図2に示す質量m₁，m₂および質量のない剛体棒l₁，l₂からなる2重振り子の運動方程式を導くことにする。

図2　2重振り子［クリックで拡大］

　一般座標θ₁，θ₂を図のように取り、m₁，m₂の速度をv₁，v₂とする。v₂はm₁回りのm₂の速度

とv₁の合成されたものであるから、

式31

となる。また、これから運動エネルギーは、

式32

となり、位置エネルギー（静止状態をゼロとして）は、

式33

となる。以上を式23に代入すると、2重振り子の運動方程式が求まる。すなわち、

式34［クリックで拡大］

から

式35［クリックで拡大］

となる。前々回の回転2関節機構の運動方程式は、同様の手順で求めたものである。上式は大振幅振動にも適用できる非線形方程式であるが、微小振動の場合は線形化して下式となる。

式36