ラグランジュの方程式（その2）〜ラグランジュの方程式の導出手順と適用例〜：1Dモデリングの勘所（40）（2/5 ページ）

「1Dモデリング」に関する連載。連載第40回では「ラグランジュの方程式（その2）」と題し、ラグランジュの方程式の導出手順とその結果を具体事例に適用して効果を確認する。さらに、ラグランジュの方程式を粘性減衰がある場合に拡張し、実際の問題に適用してみる。

[大富浩一／日本機械学会 設計研究会，MONOist]

　一方、保存系において、系の位置エネルギーが力のポテンシャル

式19

の場合、力の成分は、

式20

で与えられる。これを一般力の式に代入すると、

式21

となる。ポテンシャルから導かれる式20の一般力を分離し、その他の成分をQ_orと置くと、

式22

となり、式18は、

式23

となる。Uは質点の位置により決まり、一般座標q_rのみの関数で、一般速度

は含んでいないため、

式24

となる。ここで、

式25

と置くと式23は、

式26

となる。保存系の場合には、Q_or＝0なので、

式27

となる。Lをラグランジュ関数またはラグランジュアンと呼ぶ。

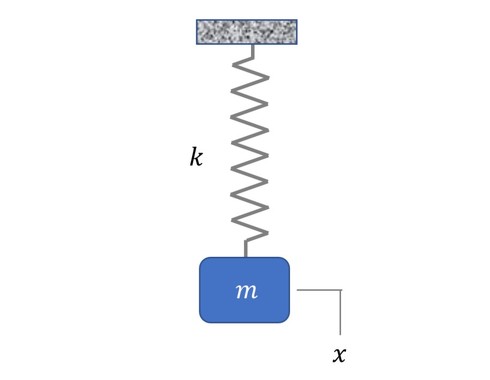
　以上を、図1に示す簡単な1自由度系で試してみる。ここで、ラグランジュの方程式は、

式28

となる。このとき、

式29

となり、これを上式に代入して偏微分すると、

式30

を得る。

図1　マスとばねからなる1自由度振動系［クリックで拡大］