【総まとめ】CAEと疲労強度計算について振り返る：CAEを正しく使い疲労強度計算と有機的につなげる（19）（2/4 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。最終回となる連載第19回では、連載の総まとめとしてこれまでの内容を振り返る。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

100％片持ちはり

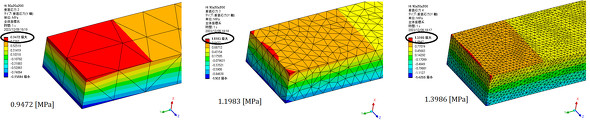
　誰が見ても「これは片持ちはりだ」と判断できるような例を使って、CAE解析のトラップを紹介しました。そのトラップの主たるものは「応力特異点」でした。図1に応力特異点の例を再掲します。

図1　応力特異点の例［クリックで拡大］

　片持ちはりの計算式から、根元の応力は0.918［MPa］ですが、図1では要素分割を細かくしていくと応力値が0.94［MPa］、1.20［MPa］、1.40［MPa］と上昇しました。図1右図の例では、はり理論から50［％］も大きな値となりました。片持ちはりの根元は応力特異点と呼ばれる状態となっており、応力特異点の応力値がだんだんと大きくなる理由を、以下のように説明しました。

• 物体の角部には応力集中が発生して応力が大きくなる
• 角部の曲率半径をRとするとRがゼロに近づくと弾性力学方程式による応力値は無限大に近づく
• 有限要素法ソフトはある条件を満足しているときは、要素分割を細かくしていくとその解は弾性力学の厳密解に近づく
• 安易な境界条件を設定すると、片持ちはりの根元の曲率半径Rがゼロの状態を作ってしまう
• 要素分割を細かくすると有限要素法ソフトが出力する応力値は無限大に近づく。つまり、だんだん大きくなる

　応力特異点の異常な応力値は、気付かれずにスルーされることがほとんどですが、これが疲労破断箇所だとすると、詳しく解析、つまり要素分割を細かくして解析されます。前述のように要素分割を細かくすればするほど応力値は大きくなるので、有限要素法ソフトの出力が信じられなくなります。

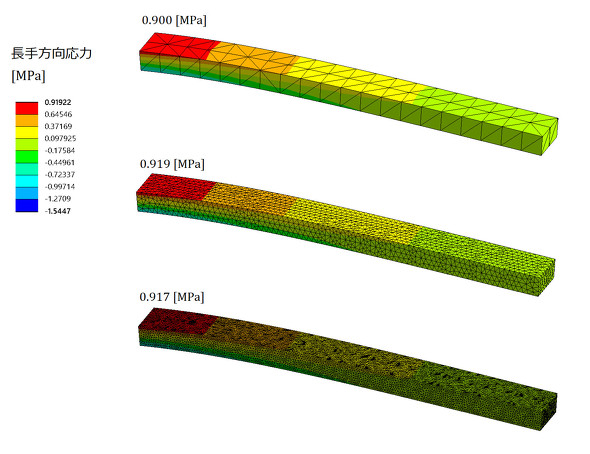
　応力特異点の回避方法の1つ目は、境界条件の設定法にありました。適切な境界条件だと、図2に示すように要素分割が変わっても応力値は同じ値となり、かつはり理論による応力値と一致します。

図2　解析結果［クリックで拡大］

　2つ目の方法は回避方法とは少し異なりますが、切欠係数βを用いる方法です。応力集中係数αと切欠係数βの定義を以下に記します。

式1

式2

　応力特異点の応力集中係数は無限大なので、応力特異点の応力解析値を使った強度計算は破綻します。しかし、疲労破断のための強度計算では切欠係数βを使うことができます。Rがゼロの部材の切欠係数は、400［MPa］級の鉄鋼ではβ＝2.4［-］くらい、600［MPa］級の鋼棒ではβ＝3.3［-］だということを連載第9回で述べました。つまり、応力特異点の切欠係数βは、2.4［-］や3.3［-］であるということです。

　切欠係数を使った疲労強度計算では、公称応力（応力集中成分を含まない応力）を使います。応力特異点を含む解析モデルでは、公称応力の代用であるポットスポット応力を求めて、これと「材料の疲労強度をβで割った値」とを比較すれば疲労破壊の有無を予測できます。このようにすると、応力特異点の応力を求める必要はなくなりました。

　この方法は、強烈な応力集中が発生している部品の疲労強度判定にも使えます。ホットスポット応力と切欠係数を使うことで、応力集中部の応力を正確に求める必要はなくなりました。有限要素法は応力集中部の応力を求めることが得意だったのですが、得意分野を生かせないのは少し残念です。