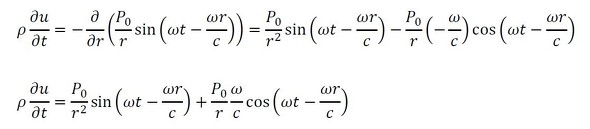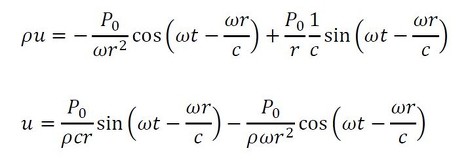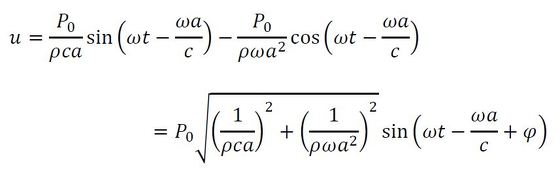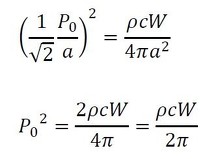騒音シミュレーション事例:CAEと計測技術を使った振動・騒音対策(20)(1/4 ページ)
“解析専任者に連絡する前に設計者がやるべきこと”を主眼に置き、CAEと計測技術を用いた振動・騒音対策の考え方やその手順を解説する連載。連載第20回では、騒音シミュレーションの事例をいくつか紹介する。
今回は、騒音シミュレーションの事例をいくつか紹介します。
球面音波
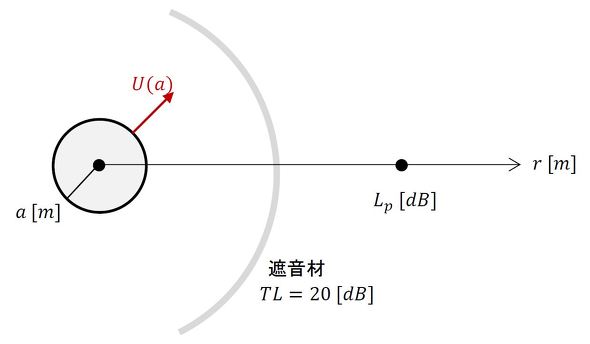
図1に示したような出力W[W]の点音源から距離r[m]離れた点の音圧レベルを計算してみましょう。ついでに等価損失が20[dB]の遮音材も考慮しましょう。点音源だと都合が悪いので音源は半径aの球とします。
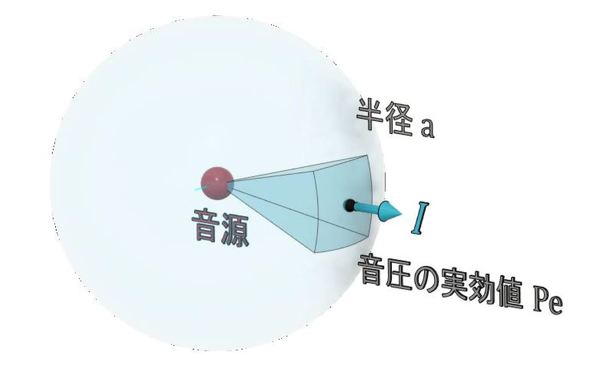
図2に半径aにおける音の強さ(音響インテンシティ)を示します。赤色の点が半径0の点音源、水色の球が半径aの音源とします。
点音源と同じ音響出力を持つ球音源の粒子速度を求めます。粒子速度がシミュレーションでの音源の境界条件となります。半径aにおける音響インテンシティはWを球の表面積で割った値なので次式となります。
平面音波と球面音波では大事な関係式がありました。次式です。
式2に式1を代入すると、音圧実効値は次式となります。
球面音波の波動方程式は次式となります(参考文献[1])。
波動方程式の2つの解のうち、広がっていく波動方程式の解は次式となります。
正弦音波と仮定すると、波動方程式の解は次式で表現できます。
微小な空気の立方体の運動方程式は、連載第2回の内容を参考にすると次式となります。
式7に式6を代入します。
式8を時間tで積分します。
r=aを代入し、sinとcosの合成式を使います。
r=aにおける音圧振幅はP0/aなので、音圧実効値は次式となります。
上式と式3が等しいとすると、次式が成立します。
式10に上式を代入します。
r=aにおける流体粒子の速度振幅は次式となります。この速度振幅がシミュレーションの境界条件となります。
半径rでの音圧レベルLpは、音圧レベルの定義式と式3から次式で求められます。
参考文献:
- [1]小橋豊|基礎物理学選書4 音と音波|裳華房(S62)
Copyright © ITmedia, Inc. All Rights Reserved.