低次元化モデリング(ROM)をさまざまな視点から考える:1Dモデリングの勘所(16)(1/4 ページ)
「1Dモデリング」に関する連載。連載第16回は「低次元化モデリング(ROM)」をテーマに、その定義や次元化モデリングの方法、さらには低次元化モデリング手法をうまく使いこなすための留意点について解説する。
今回は「低次元化モデリング」について考える。低次元化モデリングとは、連載第4回でも紹介したように「1Dモデリング」の一手法である。低次元化モデリングは英語で「Reduced Order Modeling」や「Model Order Reduction」といわれている。本稿では、英語で略して表現する場合には「ROM(Reduced Order Modeling)」とする。
最初に、低次元化モデリングの定義について考え、次に低次元化モデリングの方法を紹介する。続いて、代表的なROM手法を2つ取り上げる。最後に、低次元化モデリング手法をうまく使いこなすための留意点について述べる。なお、本稿では1Dモデルによるシミュレーションツールを「1D-CAE」、3Dモデルによるシミュレーションツールを「3D-CAE」と呼ぶことにする。
低次元化モデリングとは
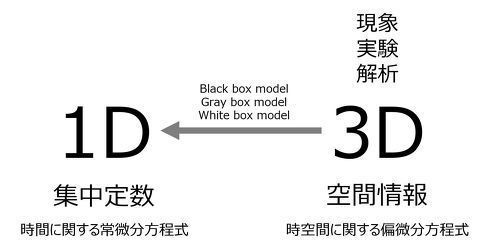
図1に、低次元化モデリングの定義を示す。言葉が示す通り、3D-CAEや実験などによる3D情報を、1D-CAEに入力可能な1D情報に変換することを「低次元化」と呼ぶ。別の言い方をすると、時空間に関する偏微分方程式を時間のみに関する常微分方程式に変換する行為ともいえる。
世の中には、ROMと称してさまざまな手法が存在するが、中には実体がうまく1Dに投影されないモデリング(Black Box Model)も存在する。本稿の最後で述べるが、モデリングはそれ自体が最終目的ではなく、モデルを用いて対象製品をデザインすることが目的であるので、これに適さないモデリング方法はここでは対象外とする。
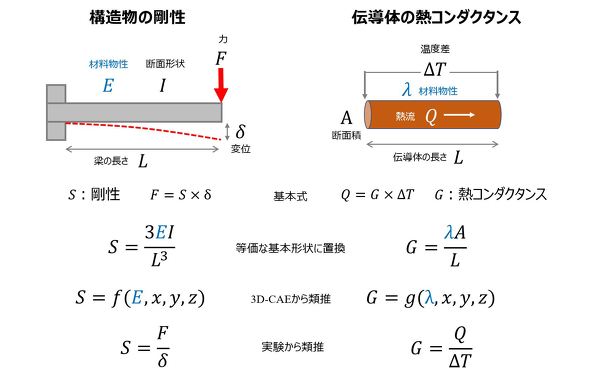
図2に、さまざまな低次元化モデリング手法を“構造物の剛性”“伝導体の熱コンダクタンス”を例に示す。対象物を等価な基本形状に置き換えて、それぞれの現象を表現する基本式にのっとって表現する方法が最もシンプルで分かりやすい。簡単な式で表現されるため、直感で現象を理解できる。
一方、実際の問題では、基本形状で置換することができない場合があるのも事実である。このようなときには、3D-CAEを用いて、剛性の場合には力と変位の関係、熱コンダクタンスの場合には熱量と温度差の関係から類推することが可能である。また、実験によっても、力と変位、熱量と温度差を計測して、剛性または熱コンダクタンスを求めることができる。
一般には、3D-CAEや実験を基に低次元化することをROMと呼んでいる場合が多いように思われるが、基本は等価な基本形状に置換することである。なお、ここで重要なのは、3D-CAEや実験の場合には物性値、形状情報が表からは見えないことで、こうした場合には以下のように無次元化することが望ましい(式1)。
こうすることによって、材料が変わっても、形状がある程度変わっても求めたい特性を予測することが可能となる。
図2に示したように、低次元化モデリングでは対象とする現象を支配する力学(方程式)を把握した上で、これを構成する特性、さらには特性を支配する物性、形状を理解しておくことが重要である。
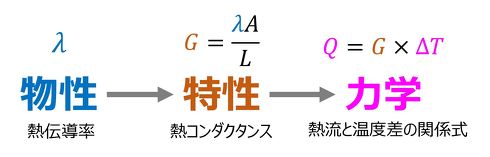
図3に、現象(力学)と物性、特性の関係を示す。すなわち、熱伝導率という物性と形状から熱コンダクタンスという特性が定義され、これが熱流と温度差の関係式の比例定数となる。
Copyright © ITmedia, Inc. All Rights Reserved.