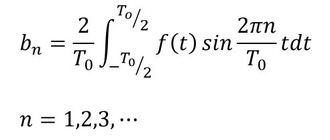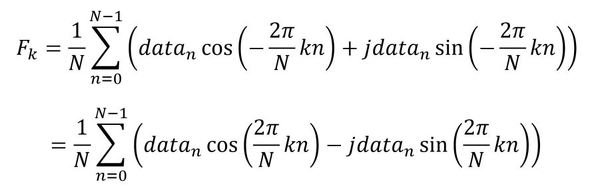振動・騒音対策の前に「周波数分析」の必要性と原理を理解する:CAEと計測技術を使った振動・騒音対策(4)(3/4 ページ)
連載「CAEと計測技術を使った振動・騒音対策」では、“解析専任者に連絡する前に、設計者がやるべきこと”を主眼に、CAEと計測技術を用いた機械の振動対策と騒音対策の考え方や、その手順について詳しく解説する。連載第3回では「周波数分析」について取り上げる。
フーリエ級数、フーリエ変換、離散フーリエ変換
FFTアナライザを使って周波数分析をするのですが、FFTとは「Fast Fourier Transform」の略です。フーリエという名前が出てきましたね。FFTアナライザはフーリエ変換ではなく、「離散フーリエ変換」をすることで周波数分析を行います。厳密なことは参考文献[1][2]をご覧いただくとして、ここでは簡単に紹介します。
フーリエ級数とは、式7で定義される三角関数で構成される級数です。
式7の係数anとbnを「フーリエ係数」といい、次式で求まります。
連載第2回で説明したように、1次元の波動方程式(シュレディンガーではない方の波動方程式です)を解くときに、フーリエ級数を使います。さらに、熱が伝わるときの温度分布を求めるときにもフーリエ級数を使います。「フーリエの法則」は熱流束と温度勾配を関係づける式です。フーリエ級数は「紙と鉛筆」を使って計算します。コンピュータは積分ができないので出番はありません。
式11で定義される変換を「フーリエ変換」といいます。フーリエ変換から「ラプラス変換」に発展して、これも微分方程式を解くときに使います。
電気工学科でのお話です。数学の講義のときに学生の誰かがラプラス変換を使って黒板に微分方程式を解いたのですが、これを見た教授は「教えてないぞ!」と言ったそうです。電気回路の過渡応答の計算で、ラプラス変換を先に習っていたのですね。機械工学科だった筆者は、フーリエ級数を物理の講義で知りました。昔の工学系は数学の進み方が専門科目に追い付かないことがありました。だから数学は大急ぎで進める必要があり、数Iの講義では参考文献[1]を1ページ目からはじめて、同時に数IIの講義では参考文献[1]の中間からはじめていたのでした。筆者が習った数学は18世紀ごろまでの数学のようです。フーリエさんのように、18世紀前後までは自然科学者と数学者は同一人物で、現象の解明のために数学を発展させたのでした。その後、枝分かれし、数学は純粋なものになるのですが、それらは機械工学には必要なくカリキュラムからバッサリと削られていたのでした。
フーリエ変換とラプラス変換も「紙と鉛筆」を使って計算します。コンピュータの出番はありません。というわけで、フーリエ級数とフーリエ変換は、本連載の対象外となります。
周波数分析は式12で定義される離散フーリエ変換を使います。
Σ記号の前に「1/N」を付けている書籍と付けていない書籍がありますが、「1/N」を付けるとFkが振幅となります。Excelには離散フーリエ変換する機能があり、Excelは「1/N」を付けていない値を出力します。「オイラーの公式」を使うと離散フーリエ変換は次式になります。
datanは、時間間隔Δtで測定された観測データです。観測データにコサインとサインを掛け算して総和をとっています。本稿の前半で「100[Hz]なのかな? と思ったら調べたい波形f(t)に100[Hz]のsin波を掛けて積分してみましょう」と説明しましたが、その通りのことをやっています。
周波数分析では離散フーリエ変換をするのですが、その原理はコサインとサインを掛け算して総和をとることなのです。この計算をそのまま実行すると時間がかかるので、1965年にCooleyとTukeyが発表した離散フーリエ変換を高速に計算するアルゴリズムを用います。
このアルゴリズムは「FFT(高速フーリエ変換)」と呼ばれています。インターネット上から入手できるソースコードは30行くらいでとても洗練されている代わりに、ソースコードを読んでも何をやっているのか分かりません。何回も説明していますが、コンピュータは積分ができません。不定積分をやってくれるソフトウェアがありますが、それは不定積分式を表すテキストを出力しているだけです。というわけで、FFTという表現は「フーリエ変換」と言っていて正確ではなく、「高速離散フーリエ変換(FDFT:Fast Discrete Fourier Transform)」と呼ぶべきです。FDFT……、語呂が悪いですね。
参考文献:
- [1]矢野健太郎、石原繁|解析学概論|裳華房(S53)
- [2]日野幹雄|スペクトル解析|朝倉書店(1987)
Copyright © ITmedia, Inc. All Rights Reserved.