スピーカーのモデリング〜電気、機構、音響の連成問題、3つの現象を回路で表現〜：1Dモデリングの勘所（12）（2/5 ページ）

「1Dモデリング」に関する連載。連載第12回では、スピーカーのモデリングを考える。構造／原理を確認して機能構造マップを作成し、これを基にモデリングする。その際、電気系、機構系、音響系の3つの系を回路で表現し、各系を結び付ける関係式を導出することにより、スピーカー全体系のモデリングを行い、電気系、音響系を機構系に縮約してスピーカーの伝達特性を導出する。最後に「Modelica」によるモデリング例を示す。

[大富浩一／日本機械学会 設計研究会，MONOist]

スピーカー各部の定式化

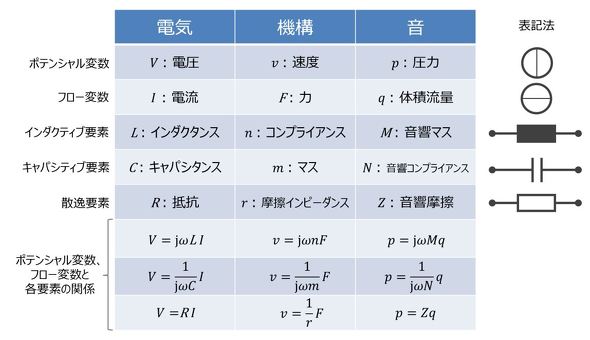
　スピーカーのモデリングでは、電気、機構、音といった異なる現象を統一的に扱う必要がある。そこで、電気回路を基本に、機構および音を電気回路に置き換える回路法を適用する。表1に電気、機構、音の各変数、各要素、変数と要素の関係を示す。このように電気、機構、音の各変数、各要素を対応付けることにより、形式的にではあるが同一形式での表現が可能となる。変数、要素に関しては、連載第9回の図10でも示したように、表1の右側の表記法を用いることにする。以下、この表記法にのっとって、電気回路、機構回路、音回路を構築する。

表1　電気、機構、音の各変数の関係［クリックで拡大］

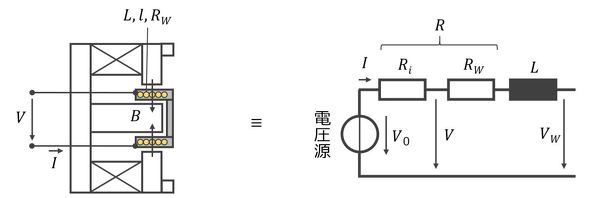
　図4に電気回路の表現結果を示す。入力電圧Vに対して、配線抵抗R_i、コイル抵抗R_W、コイルのインダクタンスLが直列に配置されている。ここで、磁石の磁束密度をB、コイル長をlとすると、コイル部には次式の力Fと起電力Vが発生する。

式1

式2

　ここでのvはコイルの振動速度である。

図4　電気回路の表現［クリックで拡大］

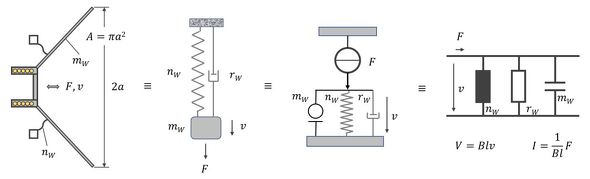
　図5に機構回路の表現結果を示す。機構回路の入力は電気回路の出力である力Fと振動速度vになる。機構を回路に置き換えるには図5に示すように、いわゆる「MCKモデル」を起点に考える。入力である力Fは機構の3要素（マスm_W、コンプライアンスn_W、摩擦インピーダンスr_W）に並列に作用し、3要素は同じ振動速度vで振動していることを、最終的な機構回路（図5右図）は示している。機構は音に対して下記の体積流量qと力F_p（圧力p）を出力する。

式3

式4

　ここでのAはコーンの面積（πa²）、pは圧力である。

図5　機構回路の表現「クリックで拡大」

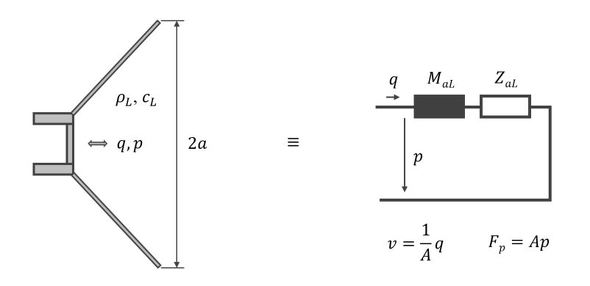
　図6に音回路の表現結果を示す。音回路の入力は機構回路の出力である体積流量qと圧力pになる。図中のZ_aLは可動空気の音響摩擦、M_aLは可動空気の音響マスで、これらは次式で定義される（参考文献［1］）。

式5

式6

　ここでのc_Lは空気の音速、ρ_Lは空気の密度、ωは角振動数である。

図6　音回路の表現［クリックで拡大］

参考文献：

• ［1］A. Lenk, Grundlagen der Akustik. Skript zur Vorlesung. TU Dresden. Institut für Technische Akustik, Dresden, 1995