ボルトが疲労破壊しない条件：設計者向けCAEを使ったボルト締結部の設計（3）（4/4 ページ）

部品の固定（締結）のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第3回は「ボルトが疲労破壊しない条件」について詳しく取り上げる。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

有限要素法で求めた締め付け線図

　前ページの表4に示したように、有限要素法で求めたボルトの変動荷重は、締め付け線図で求めたボルトの変動荷重の約13分の1なので、本稿2ページ目の図11で示した締め付け線図の被締結体側の傾きは約13倍急峻となり、締め付け線図からボルトの変動荷重を求めることができません。他の表現方法はないでしょうか。

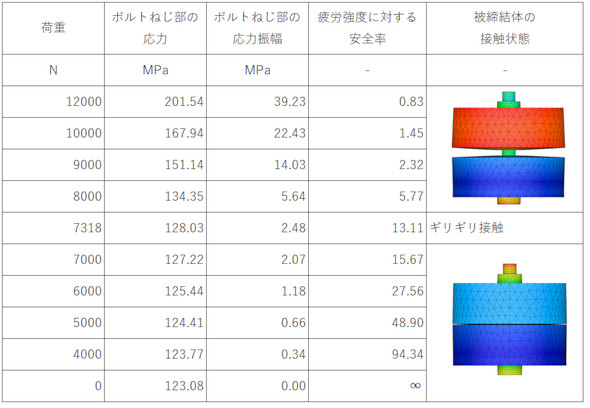
　前ページの図14の境界条件において、被締結体1に作用させた上向き荷重（荷重W）を変化させて解析してみました。その結果を表5に示します。

表5　被締結体への荷重を変化させたときのボルトの応力 ［クリックで拡大］

　解析モデルにはねじ山をモデリングしていないので、表5の応力は応力集中を考慮していない“公称応力”となります。連載第2回で求めたステンレスボルトの疲労強度は、平滑材の疲労強度を切欠係数βで割っているので、この疲労強度は公称応力と比較できます。ボルトねじ部の応力振幅は式16で計算しました。

式16

　疲労強度に対する安全率は、式17で求められます。

式17

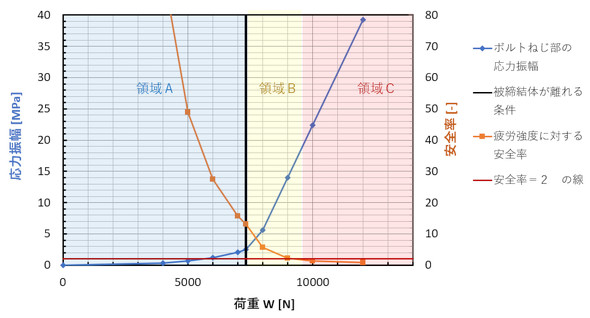
　表5の値をグラフにしたものを図18に示します。横軸は荷重W、縦軸はボルトねじ部の応力振幅と安全率です。

図18　新たな締め付け線図 ［クリックで拡大］

　応力振幅と安全率があるところを境に、急激に上昇しています。図18の黒色の線（被締結体が離れる条件）は、ボルトの初期締結力と荷重が等しい位置を示す線です。黒色の線の左側は、ボルトの初期締結力が荷重より大きく、荷重が作用しても被締結体同士は接触しています。これを「領域A」とします。黒色の線の右側は、荷重がボルトの初期締結力より大きく、被締結体同士は離れています。こちらは「領域B」と「領域C」とします。

　黄色の領域Bと赤色の領域Cの違いを説明します。共に被締結体は離れてしまっていて、応力振幅が急上昇しています。ここでは、安全率が2より大きいかどうかで分けました。領域Cは、安全率が2以下で設計としては成立しません。領域Bの安全率は2よりも大きいので使えそうですが、応力振幅が大きく変動しますので設計時の荷重見積もりが少しでも間違っていたら、ボルトは疲労破壊します。また、被締結体が離れますので部品取り付け位置がずれたり、ボルトが緩んで部品が脱落したりします。これでは危なっかしくて使えません。

　一方、青色の領域Aでは、応力振幅は低い値でほとんど変動しません。図18の黒色の線（被締結体が離れる条件）の位置で、安全率は13以上もあります。連載第2回で切欠係数βについて述べましたが、これだけの安全率があれば、βが3であろうが5であろうがもはや関係ありません。

　図18の黒色の線は、ボルトの初期締結力が変動すると左右に移動します。ボルトが適切なトルクで締め付けられていなかったり、緩みが生じていたりする場合、図18の黒色の線は左方向に移動します。すると、小さな荷重Wで領域Bや領域Cになってしまい、ボルトに発生する応力振幅が増大し、疲労破壊に至ります。これがトルク管理や緩み止めが必要な理由です。また、ボルトの軸力は「初期緩み」と呼ばれる現象によって計算値より少し低下します。よって、許容される荷重は被締結体が離れる条件よりマージンをもって小さくしなければなりません。

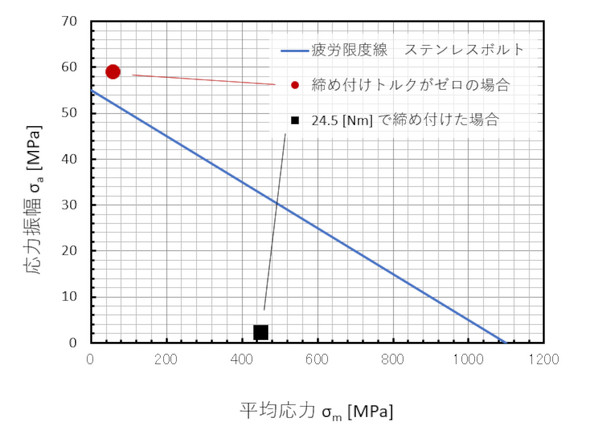
　適切なトルクで締め付けられていない場合や緩みが生じた場合を、連載第2回で解説した「疲労限度線図」を使って説明します。図19に示した疲労限度線図では、横軸を平均応力とし縦軸を応力振幅としています。

図19　M10 A2-70ステンレスボルトの疲労限度線図 ［クリックで拡大］

　青色の線は「A2-70 ステンレスボルト」の疲労限度線で、横軸切片は真破断応力、縦軸切片は連載第2回で求めた疲労強度、つまり疲労破壊し始める応力振幅です。疲労強度を求める際に、平滑材疲労強度を切欠係数βで割っているので、疲労強度は応力集中を考慮しない応力、つまり荷重振幅を有効断面積で割った公称応力と比較します。

　ある荷重条件で平均応力と応力振幅を求め、この線図上にプロットし、プロットが青色の線の上に位置したら疲労破壊します。青色の線の下に位置したら大丈夫です。

　適切なトルクで締め付けられていない極端な場合として、締め付けトルクが0の場合を考えてみましょう。荷重Wは、0〜7000［N］まで変動する繰り返し荷重とします。平均応力は7000［N］の半分をボルトの有効断面積で割って58.86［MPa］、応力振幅も58.86［MPa］となります。ボルトが24.5［Nm］で締め付けられた場合の応力振幅は、先ほどの表5から読み取って2.07［MPa］、平均応力はステンレス鋼の降伏応力450［MPa］です。これらを疲労限度線図にプロットします。

　図19に示した通り、締め付けトルクが0の場合は疲労限度線の上に位置しており「疲労破壊する」と判定できます。一方、24.5［Nm］で締め付けた場合は疲労限度線のはるか下にあり「疲労破壊しない」と判定できます。締め付けが不十分な場合や緩みが発生した場合は、2つのプロットの間に位置することになります。

　「締め付けたボルトには初期応力が作用していて、変動荷重による応力は初期応力に重畳され、締め付けたボルトが耐える変動荷重は、締め付けないボルトが耐える変動荷重よりも小さくなる」との印象は、これで吹っ飛びましたね。実際はこの反対で、締め付けたボルトの方が、大きな変動荷重に耐えることができます。

---

　以上のことが、冒頭に述べ「ボルトが疲労破壊しない条件は、変動荷重が作用したときに締結体同士が離れないこと」の理由です。このためには大きな締結力、つまりボルト軸力が必要です。次回は、軸力の見積もり方法を述べたいと思います。　（次回へ続く）

⇒「連載バックナンバー」はこちら

Profile

高橋 良一（たかはし りょういち）
ＲＴデザインラボ 代表

1961年生まれ。技術士（機械部門）、計算力学技術者 上級アナリスト、米MIT Francis Bitter Magnet Laboratory 元研究員。

構造・熱流体系のCAE専門家と機械設計者の両面を持つエンジニア。約40年間、大手電機メーカーにて医用画像診断装置（MRI装置）の電磁振動・騒音の解析、測定、低減設計、二次電池製造ラインの静音化、液晶パネル製造装置の設計、CTスキャナー用X線発生管の設計、超音波溶接機の振動解析と疲労寿命予測、超電導磁石の電磁振動に対する疲労強度評価、メカトロニクス機器の数値シミュレーションの実用化などに従事。現在ＲＴデザインラボにて、受託CAE解析、設計者解析の導入コンサルティングを手掛けている。⇒ ＲＴデザインラボ