3D CADで設計の総仕上げ!! 動きや質感まで確認してみよう／そして、次のDIYへ：ステイホームでDIYを極める！ 玄人志向なモノづくり（4）（4/4 ページ）

ステイホームで注目を集める「DIY」をテーマに、設計から製作までのプロセスを、実際の製造業におけるモノづくりの視点を交えながら解説することで、DIY素人の皆さんに“玄人のエッセンス”を伝授する。第4回は、前回に引き続き「Fusion 360」を使って設計を進め、総仕上げに入っていく。そして、後半は新たなDIYテーマの構想検討に着手する。

[藤崎 淳子／Material工房・テクノフレキス，MONOist]

2枚の板をどの位置で交差させるか

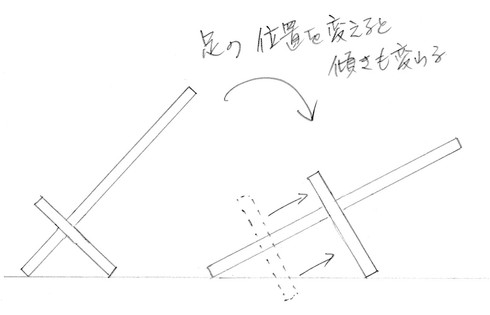
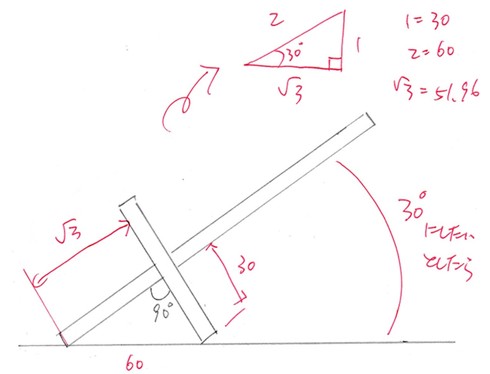
　ここまでアイデアを詰めたところで考えたいのは、「2枚の板をどの位置で交差させるか」です。背板と支えの板は直角で交差します。そして、猫のつま先に近い位置で交差させるほど背板は起き上がり、つま先から遠ざけるほど背板は寝るようになります。絵にするとこんな感じです。

図19　2枚の板をどの位置で交差させるか ［クリックで拡大］

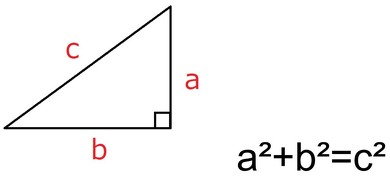
　背板をどのくらい傾けたいのかを考えて、支えの板の寸法と交差の位置を決めます。そこで使いたいのが中学校の数学で勉強した「三平方の定理」、別名「ピタゴラスの定理」です。これは直角三角形の3辺の長さに関する定理ですよね。直角三角形の直角を挟む2辺をa、bとし、斜辺をcとすると、

図20　三平方の定理 ［クリックで拡大］

の等式が成立します。

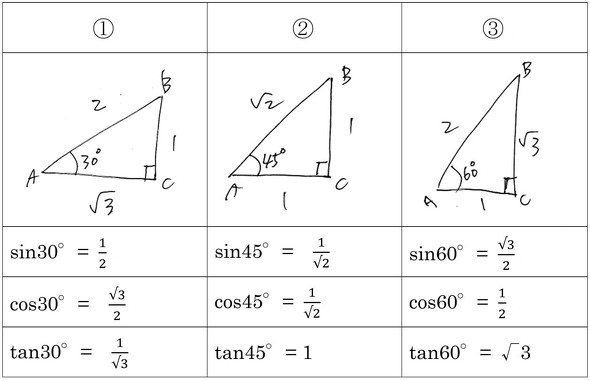
　直角三角形といえば、三角定規がそうです。もし手元にあれば見てみてください。直角以外の2つの角度が30度と60度になっている①と③では、辺の比が1：2：√3になり、直角二等辺三角形の②では、1：1：√2になります。DIYでもこの角度と辺の比の関係は必要になるものなので、ぜひ覚えておきましょう。

　三平方の定理に「三角比」を添えた表を作ってみました（表1）。これを手掛かりにして背板の傾きを計算するのです。ただ、さすがに暗算や筆算では厳しいので、「√」が計算できる電卓を用意しましょう。スマホアプリにも良い電卓がいろいろあります。

表1　三平方の定理に「三角比」を添えた表 ［クリックで拡大］

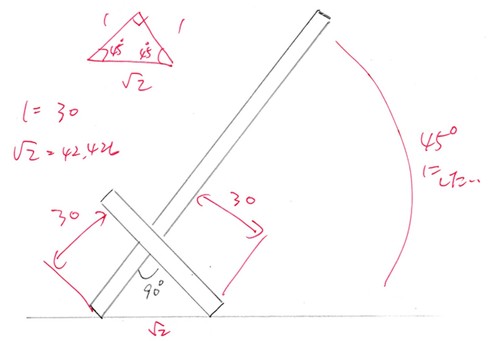
計算例（1）

　√2の値は、30√2で求めます。

図21　計算例（1） ［クリックで拡大］

計算例（2）

　√3の値は、30√3で求めます。

図22　計算例（2） ［クリックで拡大］

---

　次回は、ポンチ絵をベースに背板の傾きを検討しながら、Fusion 360を使って設計を詰めていきます。そして、実物の製作までを一気に進めます。　（次回に続く）

⇒ 連載バックナンバーはこちら

Profile

藤崎淳子（ふじさきじゅんこ）

長野県上伊那郡在住の設計者。工作機械販売商社、樹脂材料・加工品商社、プレス金型メーカー、基板実装メーカーなどの勤務経験を経てモノづくりの知識を深める。紆余（うよ）曲折の末、2006年にMaterial工房・テクノフレキスを開業。従業員は自分だけの“一人ファブレス”を看板に、打ち合せ、設計、加工手配、組み立て、納品を一人でこなす。数ある加工手段の中で、特にフライス盤とマシニングセンター加工の世界にドラマを感じており、もっと多くの人へ切削加工の魅力を伝えたいと考えている。

・筆者ブログ「ガノタなモノづくりママの日常」