位置公差の総仕上げと振れ公差について 〜曖昧さを取り除く幾何公差〜:産機設計者が解説「公差計算・公差解析」(15)(1/4 ページ)
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。最終回となる第15回は「位置公差」の残りと「振れ公差」について取り上げ、幾何公差の解説をまとめます。
前回は「位置公差」において関連性のある「最大実体公差方式」について解説しました。今回は位置公差の残りと、「振れ公差」を取り上げ、幾何公差についてまとめます。いよいよ本連載も最終回です!
2−2.同心度(中心点に対して)
Concentricity(with respect to the center point)
まずは「同心度」の定義を見てみましょう。「JIS B 0621:1984 幾何偏差の定義及び表示」(以下、JIS)によると、
平面図形の場合には、データム円の中心に対する他の円形形体の中心の位置の狂いの大きさを同心度という
と同軸度の備考として記述、定義されています。
2−3.同軸度(中心軸に対して)
Concentricity(with respect to the center line)
続いて「同軸度」です。JISによると、
データム軸直線と同一直線状にあるべき中心軸のデータム軸直線からの開きの許容値
と定義されています。
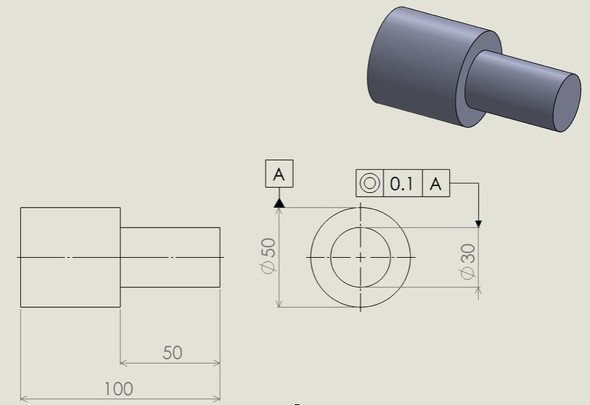
同心度と同軸度は、円柱形状の部品や円筒形状の部品で、軸の中心のズレを規定するものです。表す記号もどちらも「◎」となりますが、それぞれの違いは何でしょうか。2D図面から比較してみましょう。
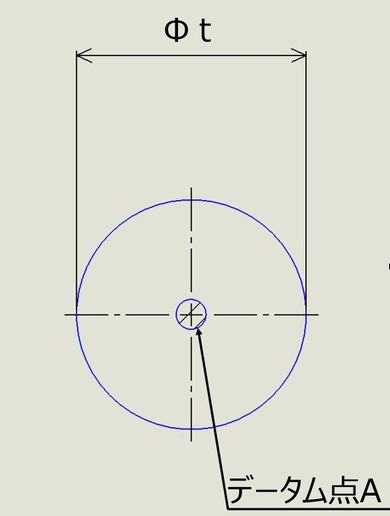
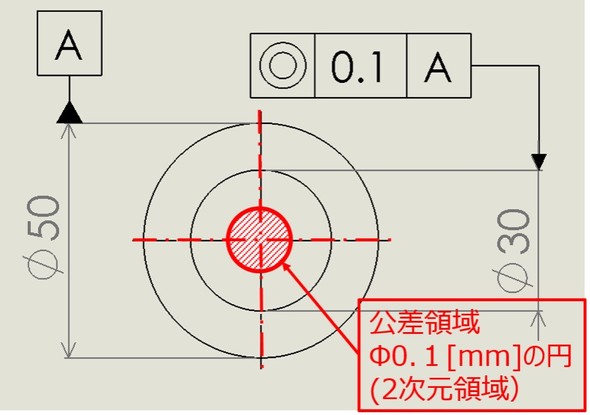
図3から、データム「中心」すなわちφ50[mm]のジオメトリ(形体)の「中心」に対して、φ30[mm]の形体の中心は、「データムと同一平面上にある直径φ0.1[mm]の円の領域(2次元)」にあるということになり、その説明は図4で表せます。
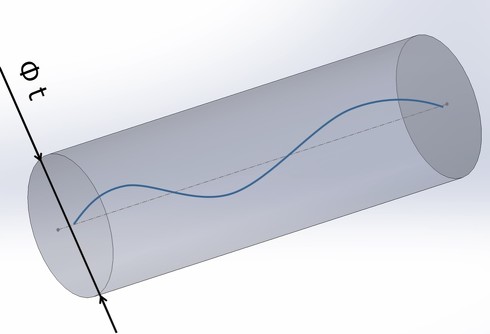
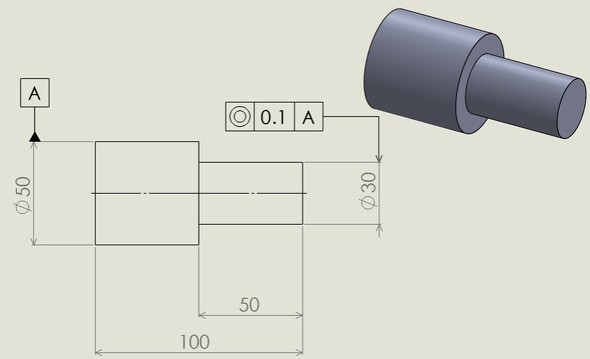
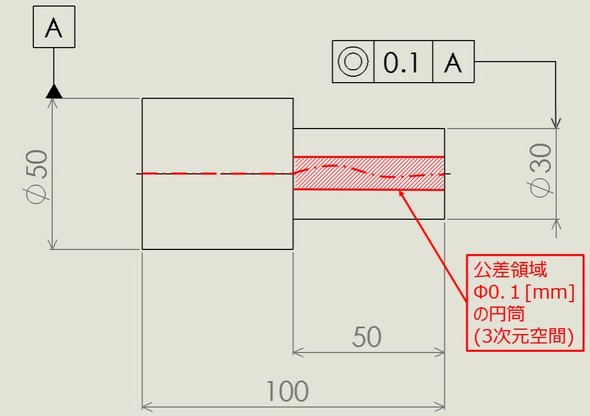
次に図5から、データム「中心軸」すなわちφ50[mm]のジオメトリ(形体)の「中心軸」に対して、φ30[mm]のジオメトリの「中心軸」は、データムと「同一直線状にある直径φ0.1[mm]の円筒内の領域(3次元空間)」にあるということになり、これは図6で表せます。
以上から、同心度と同軸度の違いは、
- 同心度はデータムに対する中心の領域を規定する ⇒ 2次元領域
- 同軸度はデータムに対する中心軸の領域を規定する ⇒ 3次元領域
となります。
では、参考にした段付きの軸部品の場合、同心度、同軸度のどちらを使うべきでしょうか。筆者の考えですが、図3のように奥行きの長さがある場合は、同心度は使わずに、同軸度を使用した方がよいと思います。
Copyright © ITmedia, Inc. All Rights Reserved.