3σと不良品発生の確率を予測する「標準正規分布表」:3D設計推進者の眼(31)(1/4 ページ)
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。
バラツキの要因「4M」
前回は、正規分布を説明する上で必要となる用語について話しました。ここで話をしていたのは、“バラツキ”についてでした(連載バックナンバーはこちら)。
さてバラツキの要因は何だったでしょうか? まずは復習です。バラツキの要因は「4M」です。
これらの要因によって、加工されるものにはバラツキが生じます。
ところが「今の時代、バラツキ0でモノが作れる」と言う人はいないでしょうか? 確かに、最新の技術、最新の設備、最適な環境下で製造することによって、そのバラツキは最小限になるのでしょう。しかしどんなに優れたツールであっても、そのツールを駆動させるための機構があり、その機構と制御によって部品は加工されます。また同一環境においても、温度というパラメータは存在します。±0℃という制御は困難ですので、部品加工においてバラツキ0というのは、あり得ない世界です。
こんな話もあります。
「今の時代、設計者の設定した公差以上の精度で加工できる」と言う人はいないでしょうか。これもまた、最新の技術、最新の設備、最適な環境下によって、結果的に設計者の設定した公差値以上の品質で部品加工できているのに過ぎません。加工コスト、加工時間、加工品質という要素が、要求仕様に見合ったものだろうかどうか、考えなければなりません。
公差は“初めに”、バラツキは“後で”
これまで正規分布のお話を多くしてきましたが、メインテーマはあくまで公差計算・公差解析のお話です。もしかしたら、“公差”と“バラツキ”を混同している人はいないでしょうか。ここで簡単に説明しましょう。
公差は、“初めに”設計者が検討して設定するものであり、バラツキは、“後で”製造後に計測されるものです。初めに設定するため「公差は要求に基づいた最適のものでなければならない」ということが理解できます。さらに「バラツキという実測値は、この公差にも反映できる」ということも分かります。
私が言いたいのは、「公差を決める公差設計の場面において、ただ単に最新の機械設備があるからということで公差を厳しくするのではなく、そのバラツキの結果に基づいて議論されるべき」ということなのです。
更には、その議論に基づく、設計者が設定する公差へのフィードバックもあり得る。これが公差のPDCAとも言えます。それについては次回以降であらためてお話しします
標準偏差と確率
今回も正規分布の話を続けます。正規分布のお話では、1σ(イチ・シグマ)、2σ(ニ・シグマ)、3σ(サン・シグマ)、6σ(シックス・シグマ)というような語句を良く聞きます。
さて、これは何を示しているのでしょうか? 前回、「ヒストグラムは、全てに対して分布を見るもので、どこに分布が集中しているのか、どこに分布がないのかを見るものです」という話をしましたが、これを更に説明すると、ヒストグラムの中には全ての分布が示されていることから、「正規分布のヒストグラムの面積は100%である」ということが言えます。
σは標準偏差といい、ばらつきの大きさを数値化したもので、個々のデータの全部の偏差を求めた後に、その平均を取って測定データの偏差の平均を“ばらつきの大きさの平均値”としたものでした。
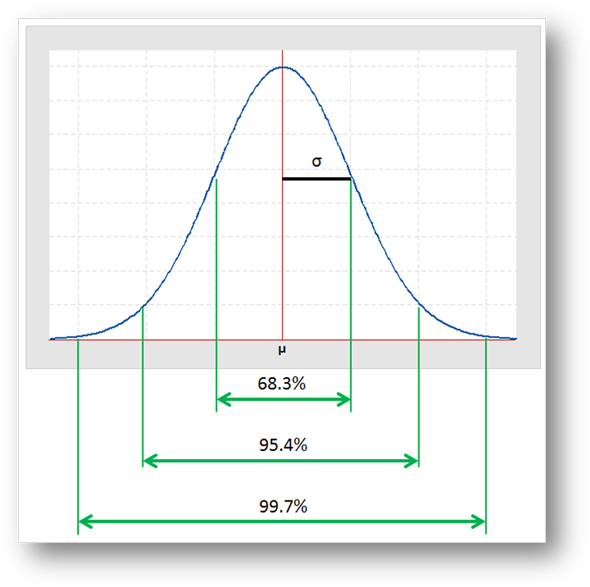
では、±σ、±2σ、±3σという範囲の面積には、正規分布のヒストグラムの総面積100%に対して、どれくらいの測定データが存在するだろうかという確率は、統計学的に、その平均値μを中心として、それぞれの標準偏差において、同じ確率となります。言い換えると、横軸の目盛がどうであろうと、同じということです。これらの確率というものは「標準正規分布N(0,12)」より求められています(標準正規分布については後述)。
- ±σ(σ区間):68.3%
- ±2σ(2σ区間):95.4%
- ±3σ(3σ区間):99.7%
- ±6σ(6σ区間):99.9997%
図示化してみると次のようになります。
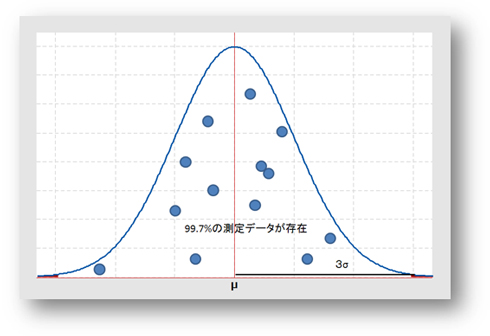
例えば、ヒストグラムから得られた正規分布曲線の領域100%に対して、3σ区域(±3σ)には、99.7%の確率で測定データが存在している(存在していなければならない)ということになります。
ちなみに、3σ区域(±3σ)では、この領域から外れる確率は「3/1000」、つまり「1000個のうち3個」ということになります。6σ区域では「3/1,000,000」、つまり「百万個のうち3個」という非常に小さな確率になります。
このように、統計学的に標準偏差からデータの存在する確率が分かることから、
その逆に、“任意に設定する数値以上”もしくは“任意に設定する数値以下”のものが存在する確率が分かりそうだ、ということが理解いただけることと思います。
正規分布からは、任意に設定した製品規格から外れる確率を求めることが可能です。一例としては、「加工部品に設定された寸法公差から外れる」ことが挙げられます。それにより不良品が発生する確率を統計学的にも求められ、よってその考え方が、公差計算・公差解析における「不良率」の計算に結びついていきます。
Copyright © ITmedia, Inc. All Rights Reserved.