実務で使う場合の線膨張係数とポアソン比：甚さんの「技術者は材料選択から勝負に出ろ！」（3）（3/4 ページ）

今回は、線膨張係数とポアソン比について例題を解きながら解説。学問としての知識から実務へ役立てるにはどうしたらいい？

[國井良昌／國井技術士設計事務所（Active Design Office），MONOist]

良君！　ちょい、ちょいと待っておくんなせぇ。いやぁ、オメェのこと「図面読めねぇ描けねぇ」の院卒とか、「CAEキー坊」とか、本当のことを言って悪かった！　許しちくれ。

どうしたんですか？　いきなり謝るなんて、甚さんらしくないですね。

ちょい、ちょいと休ましちくれ。

分かりました。今日はこれぐらいにして、アキバで手羽先とホッピィーでも行きますか？　僕の「頑張れ！　日本」に関する実行計画を聞いてほしいんです。

おうっ！　……っと言いたいところだけどよう、せっかくだから、もう少しポアソン比について説明してくれよぅ。その後は、焼酎のポアソン……じゃねぇ、デコポン割りでも飲むか？　あん？

　さすがに富士山麓大学・大学院を首席で卒業した良君は、実務ではどうも？　なんですが、学識はたいしたものですね。

　それでは、もう少しポアソン比について説明を続けましょう。

　実は、CAE技術者をまどわす大変困った公式（1）が存在します。有名な式であり、「CAE（コンピュータ・シミュレーション）には欠かせません」と、いいたいところの式ですが……、

　G（横弾性係数）＝E（縦弾性係数）/ 2（1＋ν）……公式（1）

　この公式ですが、困った条件が付くのです。

　この公式（1）は、材料が「等方性弾性体」においてのみ成立します。「等方性弾性体」とは、例えば鋼材の場合、第2回の「応力−ひずみ線図」における原点（0点）からσp（比例限度）の間で、強度や弾性係数が引っ張る方向に依存しません。これを、「等方性弾性体」と呼びます。

　難しいですね。

表1 特性表からのポアソン比と公式（1）によるポアソン比の比較：「ついてきなぁ！材料選択の『目利き力』で設計力アップ」（日刊工業新聞社刊）より

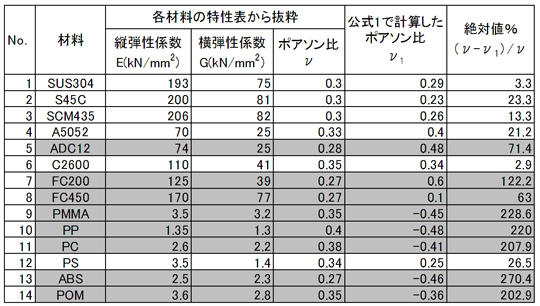
　表1のグレーの材料は、「異方性材料」、または、それに相当する材料といいます。

　「あぁ、なるほど！」と、ベテランの技術者ならば納得するデータかと思います。特性表から抜粋したポアソン比νと、計算によるν₁の値が全く合っていません。「異方性材料」であるからこの結果となりました。そして、「異方性材料」の代表的な材料が木材です。

　木材は繊維方向の引張強度が高く、繊維に直角する方向の引張強度は高くありません。このような方向に依存するような材料を「異方性材料」と呼びます。

木材を例に出すと、良く分かりますね。

そんでこの先、どうすりゃいいの？　良君。

　「異方性材料」に関して、ここで、技術の職人やCAEの方々への重要なメッセージがあります。

　特にCAE（コンピュータ・シミュレーションによる応力解析）では、材料に関する縦弾性係数や、横弾性係数や、ポアソン比等をそれぞれ定義する必要があります。それは、本サイトの材料特性から、「縦弾性係数」と「横弾性係数」から、公式（1）によるポアソン比を求めるのではなく、「縦弾性係数」と図表中に記載した「ポアソン比」をそれぞれの値で使用することを推奨します。

　筆者と親しい材料屋さんに聞きました。材料屋にとって、「等方性材料」よりも「異方性材料」の物性の測定は、はるかに骨の折れる作業とのことです。例えば、縦弾性係数を求めるより、横弾性係数の測定が困難といっていました。

従って、公式（1）は、実務での使用は、吟味しましょう。

★目利き力ポイント！：等方性材料は、G（横弾性係数）＝E（縦弾性係数）/2（1＋ν）……公式（1）

★目利き力ポイント！：異方性材料は、縦弾性係数と横弾性係数とポアソン比をそれぞれ定義する必要があり、公式（1）は吟味の上、使用する。

甚さん、分かりましたか？　これが学問です。

ばぁかも〜ん！　何の、これっしきのこと。しかし、今回はこの2つにして、主導権を再びオレサマによこせ。

ハイ、ハイ。分かりました。「職人なら、ステンレスの次にくる材料も押さえろ！」と言いたいのでしょう？