実務で使う場合の線膨張係数とポアソン比：甚さんの「技術者は材料選択から勝負に出ろ！」（3）（2/4 ページ）

今回は、線膨張係数とポアソン比について例題を解きながら解説。学問としての知識から実務へ役立てるにはどうしたらいい？

[國井良昌／國井技術士設計事務所（Active Design Office），MONOist]

前ページ問題の解答

SUS304の場合、図1に記載される線膨張係数は、17.3×10⁻⁶/℃であるから、

伸びλ＝17.3×10⁻⁶×510×（38−15）＝0.20mm

となる。

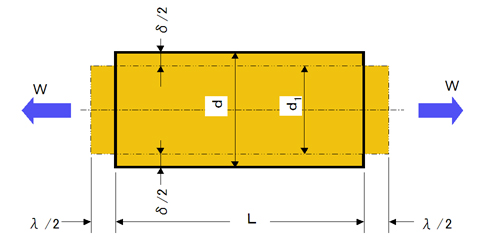
図2を参照して、ポアソン比を説明します。

図2 ポアソン比の説明図

軸方向に力（W）で引っ張ったとき、軸方向の伸び、つまり、縦ひずみ（λ/2×2＝λ）が発生します。伸びた部分があるということは、縮む（圧縮）部分もあるわけで、それが、図中のdからd₁へ縮む（圧縮）、つまり、横ひずみ（δ/2×2＝δ）が発生します。

そして、縦ひずみの「比」と横ひずみの「比」の比率を下記のポアソン比と呼びます。

• 縦ひずみの比：ε＝λ/L
• 横ひずみの比：ε₁＝δ/d
• ポアソン比：ν＝ε₁/ε

ところでよぉ、良君！　ポアソン比とはどんなとき使うんでぇ？　あん？　やさしく教えておくんなよ！

教科書には、何も書いてありません。僕が言うのもなんですが、ポアソン比とは、材料選択の「目利き力」の1つです。なぜかと言えば、CAEをかけるときの入力値であり、CAEでは不可欠の材料特性値です。

ポアソン比とは、縦弾性係数や横弾性係数と同じ「係数」です。

　係数とは計算するときに必要な「係数」です。何を計算するかと言えば、例えば、外力に対する部品の変形状態をコンピュータで計算するときの「係数」です。

　実務としての回答なら、これで十分です。

　この説明によく似たものが、「断面係数：Z」です。

図3 片持ち梁（はり）のたわみと断面係数の公式

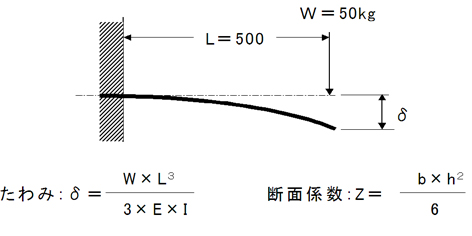
　図3は、「材料力学」もしくは、「材料工学」では必ず出てくる「片持ち梁（はり）のたわみ」の例題です。

　これを電卓で計算するには、材料の縦弾性係数（E）や断面2次モーメント（I）や断面係数（Z）を求めます。筆者が講習などでこの説明をすると、「断面係数（Z）とは何ですか？ どんな意味があるのですか？」という類（たぐい）の質問がよくきます。そのようなとき、「断面係数（Z）とは、たわみを計算するときの単なる係数です」と回答しています。ポアソン比（ν）も断面係数（Z）と同じ、単なる計算のための「係数」です。実務上は、これでよいでしょう。

ホッ！　本当は深ケー意味があるかもしれねぇけどよ、でいぶ、気が楽になっちまったぜぃ。あんがとよ。

　次に、少々学問的な角度でポアソン比の意義を解説します。まず、ポアソン比の範囲は以下となります。

1. 理論的な範囲：−1≦ν≦0.5
2. 実用的な範囲：　0≦ν≦0.5

　本連載のコンセプト（＝「親切なお料理本を目指す」）に沿って上記の2に絞ると、図4に示す各種の材料事例が提示できます。

図4 各種工業材料のポアソン比：「ついてきなぁ！材料選択の『目利き力』で設計力アップ」（日刊工業新聞社刊）より