理解しづらい傾斜度も、グループ分けでスッキリ：製図を極める！ 幾何公差徹底攻略（7）（2/2 ページ）

平行度と直角度は分かるけど、傾斜度はよく分からないという人！ ややこしく考え過ぎないで、シンプルに考えてみよう。

[山田学 ラブノーツ／六自由度技術士事務所，MONOist]

直角度

　直角度について、JISでは、「直角度（Perpendicularity）とは、データム直線またはデータム平面に対して直角な幾何学的直線または幾何学的平面からの直角であるべき直線形体または平面形体の狂いの大きさをいう」と定義されています。

　データムに対して直角であって欲しいという形体に対して指示するものです。

　平行度と同様に、加工者の不注意がない限り、旋盤やフライス盤で加工された部品の面や穴の直角が大きく崩れることは、ほとんどありませんが、設計意図を表すために必要な場合はその旨を加工者に伝える必要があります。

　寸法公差では直角のバラツキを、例えば「90°±30’」（90度±30分）のように表現できますが、直角度で指示する領域は“角度の”バラツキではなく、“領域の”バラツキであることを理解しましょう。

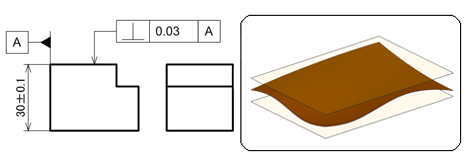
　図5に示す図面例は、ブロックの左側面をデータムとし、最上面全体がデータム平面に直角な0.03mm離れた平行2平面の中にあれば合格品と判断されるものです。

図5　直角度の指示例と領域（面指示の場合）：右側の領域を示すイラストは、データムに対して直角な平行2平面を意味します

　下面と最上面に高さの寸法公差が記入されていますが、独立の原則に従うため、高さバラツキ（±0.1mm）とは無関係にデータムA面に対する直角度を満足させればよいということです。

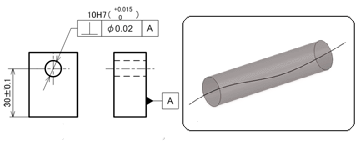
　図6に示す図面例は、右側面図におけるブロックの右側面をデータムとし、穴の中心線がデータムと直角な直径0.02mmの円柱の中にあれば合格品と判断されるものです。

図6　直角度の指示例と領域（軸線指示の場合）：右側の領域を示すイラストは、データムに対して直角な円筒を意味します

　下面と穴の中心線高さに寸法公差が記入されていますが、独立の原則に従うため高さバラツキ（±0.1mm）とは無関係にデータムA面に対する直角度を満足させればよいということです。どちらの例も、直角という姿勢だけを規制するものであって、幾何公差として位置までは規制しません。

傾斜度

　JISによると、「傾斜度（Angularity）とは、データム直線またはデータム平面に対して理論的に正確な角度を持つ幾何学的直線または幾何学的平面からの理論的に正確な角度を持つべき直線形体または平面形体の狂いの大きさをいう」と定義されます。

　データムに対して指定された角度であって欲しいという形体に対して指示するもので、平行度と直角度の違いは、指定する角度を理論寸法として四角い枠で囲って表記したものと組み合わせて使用することです。

　平行度や直角度と同様に、加工者の不注意がない限り、フライス盤で加工された部品の面や穴の傾斜が大きく崩れることは、ほとんどありませんが、設計意図を表すために必要な場合はその旨を加工者に伝える必要があります。

　寸法公差では指定された角度のバラツキを表現できますが、傾斜度で指示する領域は角度のバラツキではなく理論寸法で指示された傾きを持つ平行2平面間であり、解釈が異なることを理解しましょう。

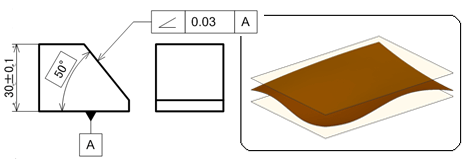
　図7に示す図面例は、ブロックの下面をデータムとし、右側の斜面全体がデータム平面に対して理論的に正しい50度の傾きを持ち0.03mm離れた平行2平面の中にあれば合格品と判断されるものです。

図7　傾斜度の指示例と領域（面指示の場合）：右側の領域を示すイラストは、データムに対して50度に傾いた平行2平面を意味します

　下面と最上面に高さの寸法公差が記入されていますが、独立の原則に従うため高さバラツキ（±0.1mm）とは無関係にデータムA面に対する傾斜度（ここでは50度）を満足させればよいということです。

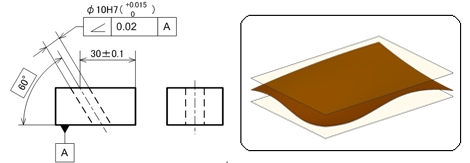
　図8に示す図面例は、ブロックの下面をデータムとし、穴の中心線がデータムに対して理論的に正しい60度の0.02mm離れた平行2平面の中にあれば合格品と判断されるものです。

図8　傾斜度の指示例と領域（軸線指示の場合 1）：右側の領域を示すイラストは、データムに対して60度に傾いた平行2平面を意味します

　右側面と上面における傾斜穴の中心軸との距離に寸法公差が記入されていますが、独立の原則に従うため距離バラツキ（±0.1mm）とは無関係にデータムA面に対する傾斜度（ここでは60度）を満足させればよいということです。

　どちらの例も、ある指定された角度という姿勢だけを規制するものであって、幾何公差として位置までは規制しません。

　このように代表的な3種類の姿勢公差を確認しました。機能上どの幾何特性を指示することが最適なのか、十分理解を深めてください。

---

　形状公差はその絶対的なカタチを、姿勢公差はデータムに対する角度を規制しました。次回は4つのグループに分類される幾何特性のうち、位置を制御する「位置公差」について解説します。位置公差である「同軸度」や「対称度」などを図面に反映させるだけで加工に親切な図面に早変わりです。設計形状に必ず要求される形状であるにもかかわらず、寸法値ではうまく表現できない場合であっても、加工者に対して設計意図を明確に伝えられます。（次回に続く）

Profile

山田 学（やまだ まなぶ）

1963年生まれ。ラブノーツ代表取締役、技術士（機械部門）。カヤバ工業（現、KYB）自動車技術研究所で電動パワーステアリングの研究開発、グローリー工業（現、グローリー）設計部で銀行向け紙幣処理機の設計などに従事。兵庫県技能検定委員として技能検定（機械プラント製図）の検定試験運営、指導、採点にも携わる。2006年4月、技術者教育専門の六自由度技術士事務所を設立。2007年1月、ラブノーツを設立し、会社法人（株式会社）として技術者教育を行っている。著書に『図面って、どない描くねん！』『読んで調べる 設計製図リストブック』（共に日刊工業新聞社刊）など。

◎併せて読みたい「CAD」関連ホワイトペーパー：

» 主要7製品を完全網羅！　製品選定・比較に役立つ「商用3D CADカタログ 完全版」

» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”

» 設計現場の56.5％が3D CADを活用、2次元からの「移行予定なし」も16.7％

» エクスペリエンス時代に向けて進化を続ける「CATIA」

» PTCが語る3D CADの歴史と「Creo」の注目機能

⇒ CAD関連の新着ホワイトペーパーはこちら