試作品の数を劇的に減らす直交配列実験の実務：Excelで学ぶ実験計画法の基礎（3）（1/5 ページ）

品質管理のための代表的な統計手法である実験計画法について、実践的な手法を短期間に習得したいと希望している読者に向けて、Excelを使って効率的に独学できるような解説を行う。

[菅民郎・福島隆司／株式会社エスミ，＠IT MONOist]

「Excelで学ぶ実験計画法の基礎」連載目次

第1回：品質管理と実験計画法の基本を押さえよう

第2回：推測統計の基礎 ―― 一元／二元配置分散分析

第3回：試作品の数を劇的に減らす直交配列実験の実務

第4回：直交配列実験を基にした重回帰分析の実務

　商品開発の品質管理の現場では、品質に影響するさまざまな要因の中から、最適な水準の組み合わせを決め、商品設計を行う必要があります。品質に影響すると考えられる要因が1つや2つであった時代は、古典的な実験計画法の知識で要因を特定することができたのですが、商品機能が複雑化した現在では、品質に影響する要因の数が増えたため、従来の方法では対応できない状況になっています。

　具体的には、実験に必要な試作品の種類が膨大となり、実験自体が不可能になる状態や、できたとしても、かなりの月日が想定されるといった状態です。製品ライフサイクルが短くなった現在、従来の方法で実験を実施していては市場環境に対応できなくなりました。このような現場の問題解決のために考案された実験計画法が、今回ご紹介する直交配列実験と呼ばれる方法です。本稿ではまず、古典的な実験計画の方法と考え方を紹介し、次に直交配列実験の方法および得られたデータの解析方法を紹介します。

要因実験の事例

　新製品の仕様を企画しています。品質に影響する2つの因子AとBにある水準の組み合わせを決めるために、試作品を作って評価実験を実施することにしました。ただし、実験の回数を減らすために、次のような計画を立てました。

• 因子Aの水準をA1に固定して、因子Bの各水準を組み合わせた試作品を作る。
• 試作品の評価を行い因子Bの最適水準を決める。
• 因子Bの水準を2で決めた最適水準に固定して、因子Aの各水準を組み合わせた試作品を作る。
• 試作品の評価を行い因子Aの最適水準を決める。

表1　当初の実験結果

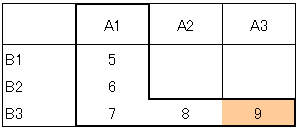
　実験の結果が表1です。因子Aの水準をA1に固定した試作品はB3の評価が最も高く、次に因子Bの水準をB3に固定した試作品の評価はA3が最も高い結果になりました。

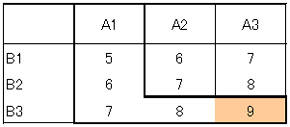
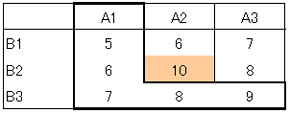
　ここで、すべての組み合わせで実験を実施した場合の結果を2つ示します。おのおので最も評価の高いセルに彩色しています。先の手順にて実験を実施した結果との対応を確認すると、表2の場合の最適水準の組み合わせは一致していますが、表3の場合、最適水準の組み合わせはA2B3で一致していません。最適水準にたどり着くとは限らない上記実験は、適切な方法でないことが分かります。

表2　すべての組み合わせで実験を実施―1回

表3　すべての組み合わせで実験を実施―2回目

　この例からいえることは、最適水準の組み合わせを特定するためには、各因子の水準のすべての組み合わせ（9回＝3水準×3水準）で実験を実施する必要があるということです。このように各因子の水準のすべての組み合わせで実験する方法を要因実験と呼びます。