直交配列実験を基にした重回帰分析の実務：Excelで学ぶ実験計画法の基礎（4）（1/5 ページ）

品質管理のための代表的な統計手法である実験計画法について、実践的な手法を短期間に習得したいと希望している読者に向けて、Excelを使って効率的に独学できるような解説を行う。

[菅民郎・福島隆司／株式会社エスミ，＠IT MONOist]

　前回の連載までに、品質に影響する因子（要因）を特定する実験計画と、得られたデータの解析の方法を紹介してきました。ところで、ある因子が品質に影響するとして、具体的にどのような影響を与えているのでしょうか。

「Excelで学ぶ実験計画法の基礎」連載目次

第1回：品質管理と実験計画法の基本を押さえよう

第2回：推測統計の基礎 ―― 一元／二元配置分散分析

第3回：試作品の数を劇的に減らす直交配列実験の実務

　最終回は、直交配列実験で実施した実験データを基に、因子が品質に影響する効果の大きさを数値化する方法を紹介します。

3因子2水準の事例

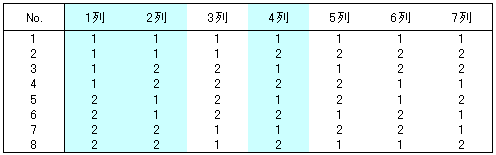
　工程の不良品個数に影響する因子を特定するために、3つの因子を取り上げて直交配列実験を計画します。各因子の水準は2つとします（図1）。

図1　3因子2水準の直交配列実験

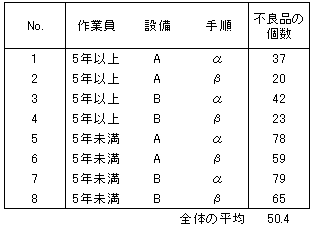
　直交表はL8直交表を選択しました。直交配列実験およびL8直交表を用いた実験計画の方法については前回「試作品の数を劇的に減らす直交配列実験の実務」の記事をご参照ください。次にL8直交表の列1、列2、列4に因子を割り付けました。L8直交表と実験の組み合わせは図2のとおりです。実験を実施した結果、図3のデータが得られました。

図2　L₈直交表

図3　実験結果

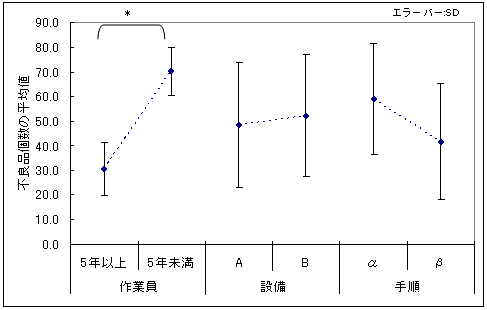
　データ解析の最初のステップは、各因子の水準の平均値の計算です。図4のような結果が得られました。

図4　水準の平均値

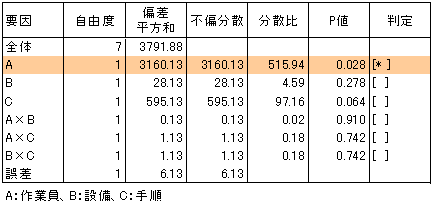
　作業員の経験年数には大きな差があり、設備と手順にはそれほど差がないように見えます。次のステップは、水準の差は統計的に意味があるのか、因子の効果の有意性の分散分析による検証です。分散分析を実施すると図5の結果が得られました。

図5　分散分析表

　「A×B」など「○×□」で表現される要因は交互作用です。交互作用については第2回を参照ください。結果を見ると、作業員の効果のみが有意水準0.05で有意でした。作業員のキャリアの違いによって不良品の個数に差があるといえます（図6）。

図6　視覚的分析

　以上は前回までの復習でしたが、実用的な問題となるのが水準の効果です。次に各因子の水準の効果を数値的に表現することを考えます。統計的には3つの因子から不良品の個数を予測する問題に帰着し、重回帰分析と呼ばれる多変量解析を利用して解決できます。重回帰分析はExcelで実行が可能です。