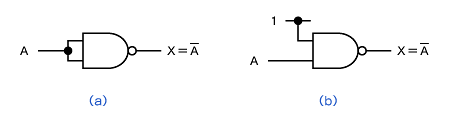知識の点検、2学期【中間考査】のお知らせ:完全マスター! 電子回路ドリル II(11)
中間考査目前の今回はNANDゲートを用いたNOT、OR、ANDの作り方を解説。これができるとどんな論理式もNANDゲートで構成できる。
【問題10】の解答
前回の宿題【問題10】は、NANDゲートを使ってNOT、AND、ORを作る問題でした。
皆さん解けましたでしょうか?
解けた方も解けなかった方も答え合わせをして、次項の解説までぜひ読んでみてください。毎週コツコツ問題を解いて、デジタル回路の基礎知識を身に付けましょう。
それでは、解答を発表します!
【問題10】の解説
【問題10】はNANDゲートを用いて、NOT、OR、ANDを作る問題です。これをマスターすると「どのような論理式もNANDゲートで構成できる」ようになります。実は、ダイオードやトランジスタを用いてゲートを実現する際、NANDはANDやORよりも扱いやすく、デジタル回路ではよく利用されているのです。
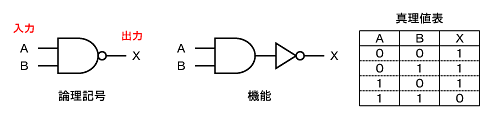
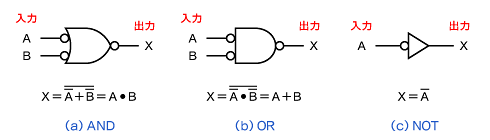
NAND(否定論理積)は、図1のようにAND(論理積)とNOT(否定)を組み合わせたもので、入力をA、B、出力をXとするとその論理式は、X = A ・ Bとなります。
NANDの論理記号は、ANDの論理記号の出力に「○記号」を付けて表しますが、この○記号は機能的にNOT(否定)を表しています。
デジタル回路において、○記号は負論理を表し、NANDに限らずよく使われています。論理記号の入力側に○記号があるときは、入力が“0(low)”で能動(active)になることを意味します。また、論理記号の出力側に○記号があるときは、その出力が“0(low)”で能動(active)になることを意味します。すなわちNANDの場合、その出力は負論理なので“0”が“真”、“1”が“偽”となり、ANDとして働いていると理解できます。
基本論理を負論理で表すと、図2のようになります。
それではNANDゲートを用いてNOT、OR、ANDを作ってみましょう。
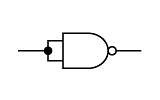
最初にNANDからNOTを作ります(図3)。
図3(a)のようにNANDの入力を接続すると、その回路はNOTとして働きます。論理式では、
X = A ・ A = A
となり、NOT(否定)となることが証明できます。
また、図3(b)のようにNANDの一方の入力を“1”に固定してもNOTになります。論理式では、
X = A ・ 1 = A
となります。
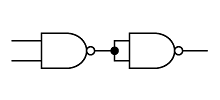
次にNAND からANDを作ります。
図4のようにNANDの出力にNOTを接続すると、その回路はANDになります。
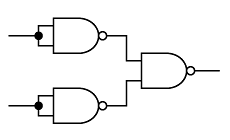
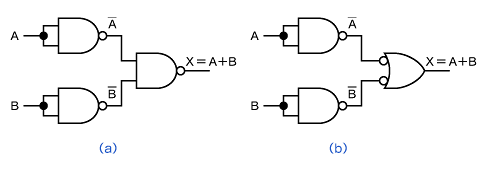
最後にNANDからORを作ります(図5)。
図5(a)のようにNANDの入力にNOTを接続すると、その回路はORになります。その証明は、「ド・モルガンの法則」により、
となります。
さらに、図5(b)のように2段目のNANDゲートを負論理で表すと、その論理式が分かりやすくなります。
次回【中間考査】のお知らせ
次回は2学期の【中間考査】を行います。いままでの連載の復習問題を掲載しますので、知識の確認のためにぜひチャレンジしてください。なお、今回の宿題はお休みとさせていただきます。
本連載「完全マスター! 電子回路ドリル II」では、デジタル回路をテーマに宿題をお届けしてきました。デジタル回路の考え方は「単純な機能を組み合わせて、より大規模で複雑な機能を実現する」ことにあります。そこに集積化技術のさらなる進歩が重なって、マイクロコンピュータのような高機能デバイスが製造できるようになったのです。
【問題1】から【問題4】までは“2進数”について出題しました。現在は、数や文字に限らず、映像や音声などの情報もデジタルで扱う時代です。そこには、2進数の考え方が応用されています。
そして、【問題5】から【問題10】までは“組み合わせ回路”について出題しました。組み合わせ回路とは、その時点の入力の値によって出力が決まる回路をいいます。この組み合わせ回路の機能を「ゲート回路」「論理式」「真理値表」の3つの表現で扱ってきました。
さて、2学期後半では組み合わせ回路に加え、“順序回路”について出題していきます。この順序回路が理解できれば、デジタル回路を完全マスターしたといえるでしょう! 継続は力なりです。どうぞ今後の宿題にもチャレンジしてください。(次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.