コイルを用いた実験回路で微分積分の本質に迫る【積分編】：今岡通博の俺流！組み込み用語解説（18）（2/2 ページ）

今岡通博氏による、組み込み開発に新しく関わることになった読者に向けた組み込み用語解説の連載コラム。第18回は、コイルを用いた実験回路を使って積分の本質に迫る。

[今岡通博，MONOist]

さまざまな波形を使って積分現象を確かめる

　今回の実験でも、筆者が所持しているハンディーオシロスコープ「OWON HDS272S」を用いて観測します。このオシロにはシグナルジェネレーターの機能があり、これで生成した信号を入力信号とします。入力信号は1Vpp（波形の振幅の山から谷までの電位差が1V）で、周波数は1kHzです。

　なお、各入力波形の説明はコンデンサーを用いた微分回路をテーマにした連載第14回を参照してください。

正弦波

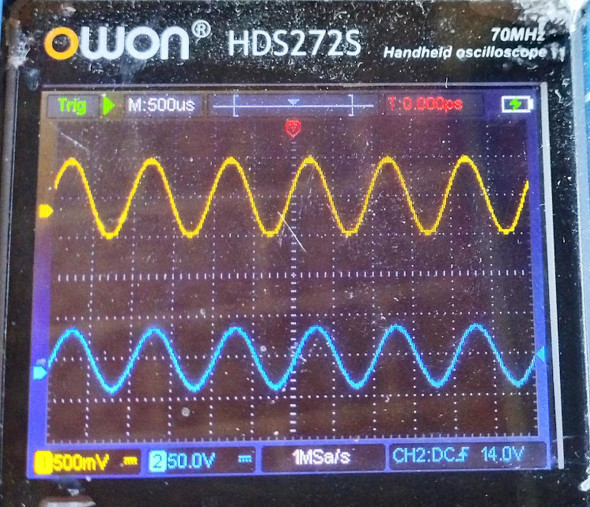
　図3は正弦波の入力波形と、積分回路を通した後の出力波形を比較するためのものです。

図3　正弦波の入力波形（上）と出力波形（下）［クリックで拡大］

　図3の波形の解釈ですが、数学で学んだところによると正弦波（sin）を積分すると負の余弦波（−cos）になります。前回紹介したコイルの微分回路では、元の波形に対して時間軸上で波が90度進んだのに対して、積分回路では90度遅れるんですね。

矩形波

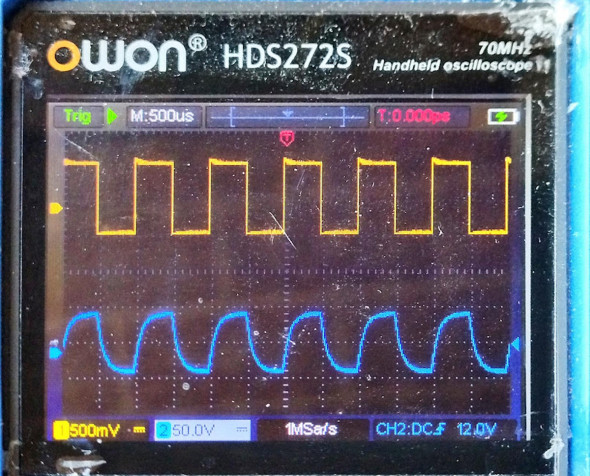
　図4は矩形波の入力波形と、積分回路を通した後の出力波形を表示したものです。

図4　矩形波の入力波形（上）と出力波形（下）［クリックで拡大］

　図4では、入力の矩形波の谷の部分でコイルは磁力を失い出力は下り坂となります。一方、矩形波の山の部分ではコイルは磁力を蓄え徐々に電圧は上がっていきます。それを繰り返すことによって三角波のような波形になっています。

ノコギリ波

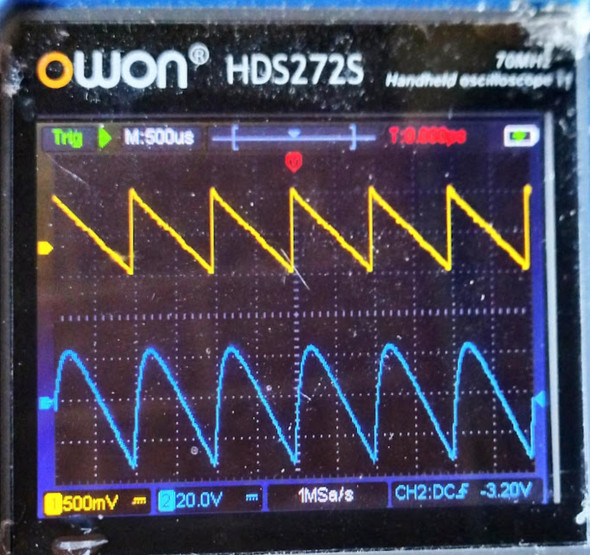
　図5はノコギリ波の入力波形と、微分回路を通した後の出力波形を表示したものです。

図5　ノコギリ波の入力波形（上）と出力波形（下）［クリックで拡大］

　図5では、入力波形のノコギリ波が急激に上昇する時点から磁力が蓄えられ多少時間差があるものの出力波形も上昇していきます。入力波形がピークを過ぎる下り坂局面でもしばらく充電は継続し、入力電圧がある一定電圧を下回るとそこをピークに電圧が下がり始めます。ノコギリ波を積分すると図5のように半円を伏せたような波形になります。ノコギリ波の上昇地点にやや偏るような波形になっていますね。

コイルの積分作用の主な応用例

　コイルの積分作用は、電圧の時間的な累積を電流として表現する性質ですので、これもまたさまざまな電気回路やシステムで活用されています。

直流電流の安定化（平滑化）

• 脈流の平滑化：整流回路（交流を直流に変換する回路）から得られる直流電圧は、実際には脈打つような変動（脈流）を含んでいます。ここにコイルを直列に挿入すると、コイルの積分作用により、この脈流の変動が吸収され、より滑らかな直流電流が得られます。コイルは電圧の急激な変化を嫌い、電流をゆっくりと変化させようとするため、脈流のピークを抑え、谷間を埋めるように作用します。
• 応用例：電源回路において、整流された直流電圧を安定させるための「平滑回路」や「LCフィルター」の一部として広く利用されています。これにより、電子機器が安定した電力で動作できるようになります。

スイッチング電源（DC-DCコンバーター）

• エネルギーの貯蔵と放出：スイッチング電源は、コイルに一時的にエネルギーを貯蔵し、必要な時に放出することで、効率的に電圧を変換する回路です。コイルに電圧をかける時間を制御することで、コイルに流れる電流（蓄積されるエネルギー）を調整し、出力電圧を安定させます。コイルは電圧の積分器として働き、入力電圧のON／OFF期間の累積に応じて電流を生成します。
• 応用例：スマートフォン、PC、LED照明など、ほとんど全ての電子機器内部で、バッテリー電圧やアダプター電圧を、各部品が必要とする異なる電圧に変換するために使われています。高効率な電力変換を実現する上で不可欠な部品です。

フィルター回路（低周波成分の通過）

• 高周波成分の抑制：コイルは、周波数が高い（＝変化が速い）信号に対しては電流が流れにくく、周波数が低い（＝変化が遅い）信号に対しては電流が流れやすい性質があります。このため、コイルを特定の回路に組み込むことで、高周波成分を抑制し、低周波成分だけを通過させる「ローパスフィルター」として機能させることができます。これは、高周波成分の「変化の速さ」を積分作用によって平滑化していると考えることができます。
• 応用例：オーディオ機器で不要な高音域ノイズを除去したり、信号から特定の周波数成分を抽出したりするフィルター回路に利用されます。

タイマー回路や遅延回路

• 電流の立ち上がり／立ち下がり時間：コイルに電圧をかけた際に電流が徐々に立ち上がる（または電圧をゼロにした際に電流が徐々に立ち下がる）性質を利用して、時間的な遅延を生成する回路を構成できます。電流が一定の値に達するまでの時間や、ゼロになるまでの時間を制御することで、タイマーや遅延素子として機能させることが可能です。
• 応用例：特定の時間遅延を必要とする制御回路や、信号のタイミングを調整する回路に利用されることがあります。

　これらのように、コイルの積分作用は、電圧の「時間的な累積」を電流として利用することで、電源の安定化、効率的な電圧変換、信号のフィルタリング、時間制御など、多岐にわたる電気／電子回路の基盤技術として応用されています。

おわりに

　今回はコイルを用いて積分作用を検討してみました。本連載ではコンデンサーによる微分と積分、そしてコイルによる微分と積分についてそれぞれ検証してきました。今回でこのシリーズはいったん区切りとなります。

　コイルやコンデンサーを含むアナログ回路を理解しようと思えば、微分積分だけではなくさらに手ごわい複素数を制する必要があります。このあたりについても、数式を使わないで説明するメソッドを思い付いたらまたご紹介したいと思います。

⇒MONOist編集部へのご意見はこちらまで