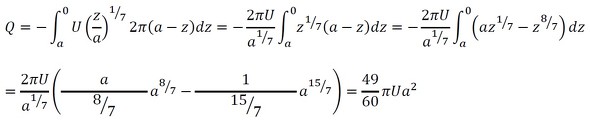乱流の円管内の流れと圧力損失の見積もり:CAE解析とExcelを使いながら冷却系設計を自分でやってみる(12)(2/4 ページ)
CAE解析とExcelを使いながら冷却系の設計を“自分でやってみる/できるようになる”ことを目指す連載。連載第12回では、乱流の円管内の流れと圧力損失の見積もりについて取り上げる。
乱流の速度分布
乱流とは何か、そして乱流シミュレーション(これは次回の話になります)についても触れなければならないのですが……筆者の理解不足もあり、正直なところ、特に次回の内容については辞退したいのが本音です。とはいえ、そうも言っていられませんので、つたないながら筆者の知識で説明を試みてみます。
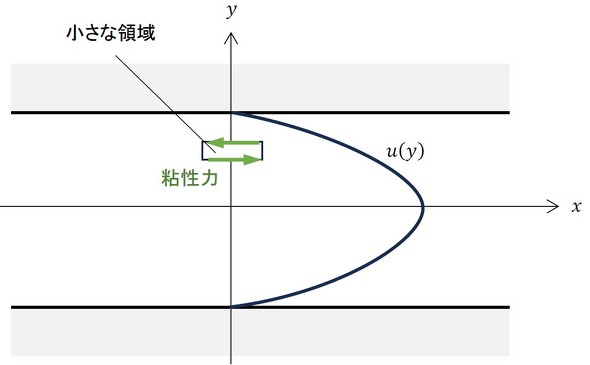
図2に、円管あるいは平行壁間における層流の速度分布を示します。
この分布は放物線の形をしています。ここで、小さな流体の領域を1つ考えてみましょう。中心付近は流速が速いため、その領域の下辺は進行方向に引っ張られます。この引っ張る力を「粘性力」と呼ぶことにします。一方、壁面では流速がゼロなので、領域の上辺は壁に引き止められようとする力を受けます。このときの粘性力は、先ほどとは逆向きになります。
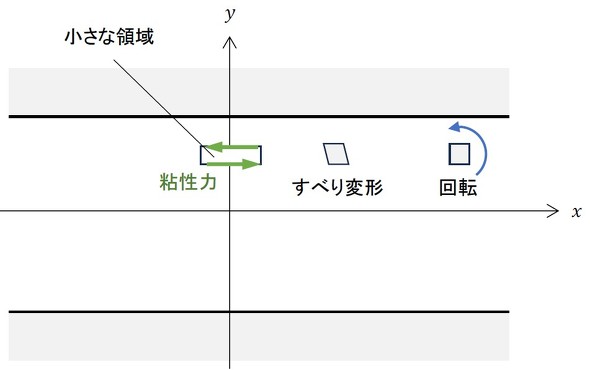
小さな領域の上辺と下辺に働く粘性力の方向が逆になるため、図3に示すように、その領域は平行四辺形のように変形します。このとき、流体の分子と分子は互いにすべり合っている状態になります。金属の塑性変形における「すべり」と似たようなものと考えています。
このすべり変形には限界があり、流速が速くなると、小さな領域は回転を始めます。この回転が「渦」です。いったん渦ができると、近くの領域にも渦が生じ、やがて流体全体は無数の渦だらけとなります。この状態が乱流と解釈しております。
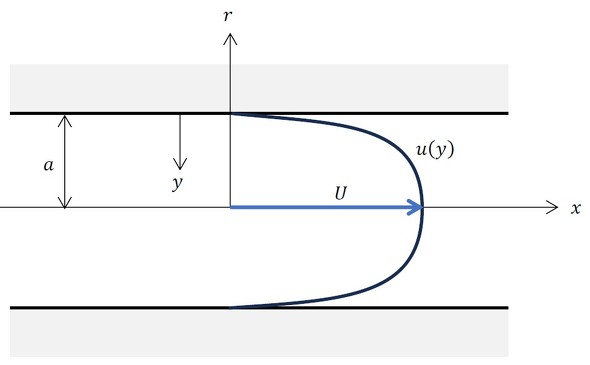
では、図2に示した層流の円管速度分布に対応する、乱流の円管速度分布はどうなるのでしょうか。これについては、「1/7乗べき則」と呼ばれる経験則があります。乱流の速度分布は、式3で近似されます(参考文献[1])。
座標の取り方に注意が必要です。yは壁面からの距離となります。y=0でu=0ですね。経験式を積分するのは少し抵抗がありますが、流量と平均流速を求めましょう。流量は式4となります。
これは置換積分ですね。z=a−rとすると、dr=−dzですね。
平均流速をumとすると、流量は式6で表されます。
式5と式6の割り算から、平均流速は式7となります。
平均流速と最大流速の比は、層流のときは1/2=0.5[-]でしたが、乱流の場合は49/60≅0.82[-]と、1に近い値となります。
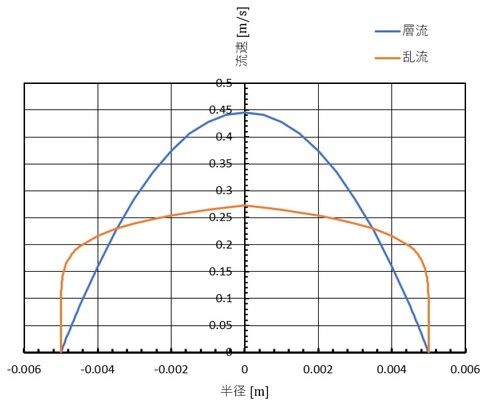
では、速度分布を計算してみましょう。図5に、円管内部の速度分布を示します。ここでは、層流と乱流で流量を同じにしています。速度分布はかなり違いますね。
たくさんの渦が下流に移動しており、例えば、渦の下側では「図5の流速+渦の回転速度」、渦の上側では「図5の流速−渦の回転速度」となるため、図5に示された流速は時間的な平均値となります。
なお、図5のグラフをぱっと見て面積が等しくないように感じるのは、円管内の流れだからです。
Copyright © ITmedia, Inc. All Rights Reserved.