連載

2025年5月16日

現象のモデリングの勘所　～現象の式のマトリクス表現～：1Dモデリングの勘所（43）（2/3 ページ）

「1Dモデリング」に関する連載。連載第43回では「現象のモデリングの勘所」をテーマに取り上げる。

LINE

Hatena

振動のMCKモデル

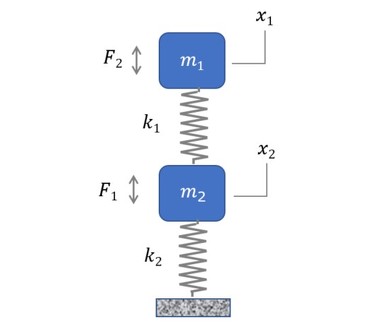
　図3に、振動の2自由度の「MCKモデル」を示す。

図3　振動のMCKモデル［クリックで拡大］

　このとき、質点1の運動方程式と質点2の運動方程式は、

式6［クリックで拡大］

となる。これをマトリクス表現すると、

図4　振動モデルのマトリクス表現［クリックで拡大］

となる。ピンク色の文字が入力で、緑色の文字が出力である。このように、現象のマトリクス表現は現象を理解するのが容易である。また、マトリクスの内部は対称行列になっている。

　続けて、熱の式も振動モデルと同様にマトリクス表現を試みる。ただし、熱の式は振動とは異なり非線形であるため、一工夫する必要がある。すなわち、ヒーターと筐体内部間のふく射による熱コンダクタンスを、

式7

と置いてマトリクス表現すると、図5となる。

図5　熱モデルのマトリクス表現［クリックで拡大］

　ご覧の通り、ジュール熱のヒーターへの入力（ピンク色の文字）が起点となって、各部の温度T₁、T₂、T₃（緑色の文字）が求まっていることが一目瞭然である。図5は3つの式からなり、当然これを解いても解は得られる。また、この場合のマトリクスの内部も対称行列となっている。

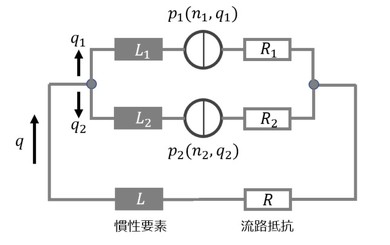
　次に、図6に示すポンプ配管系の流れのマトリクス表現を試みる。

図6　ポンプ配管系の流れモデル［クリックで拡大］

　これは抵抗要素、慣性要素、ポンプ要素からなる流路網モデルとなる。各ポンプの特性をp₁（n₁，q₁）、p₂（n₂，q₂）とする。このとき、n₁、n₂は各ポンプの回転数、q₁、q₂は流量である。主配管を流れる流量をqとすると、分岐点における流量の連続条件（電流則）から、

式8

が成り立つ。

　閉回路における圧力の閉合条件（電圧則）は、閉回路の取り方によりいくつか考えられる（当然のことながらどれをとっても結果は同じである）が、ここでは、ポンプ1＋主配管、ポンプ2＋主配管を取ることにする。

　すると、次の2式が求まる。

式9

式10

　以上を基にマトリクス表現すると図7となる。この式も非線形であるため、流量の絶対値表現の部分をその他と分離している。

図7　流れモデルのマトリクス表現［クリックで拡大］

　この場合もポンプが入力で、その結果として流量が発生（出力）していることが分かる。また、マトリクスの内部は対称行列になっている。