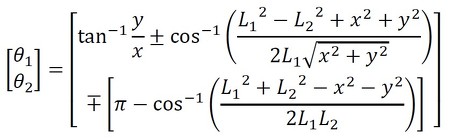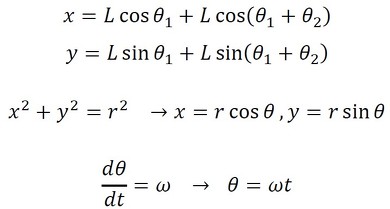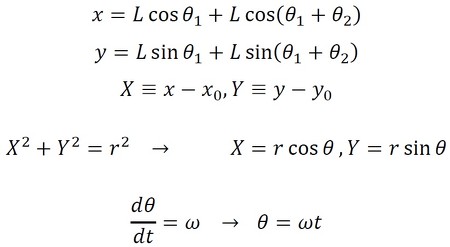機構制御系のモデリング（その3） 〜回転2関節機構の運動学・動力学を考える〜：1Dモデリングの勘所（38）（2/5 ページ）

「1Dモデリング」に関する連載。連載第38回では「機構制御系のモデリング（その3）」と題し、回転2関節機構の運動学、動力学を考えるについて考える。

[大富浩一／日本機械学会 設計研究会，MONOist]

運動学（逆問題）

　図2で先端の位置を（x，y）にするために、駆動部（θ₁，θ₂）をどう動かしたらいいかを考えるのが逆運動学で、順運動学の式のθ₁，θ₂について解く必要がある。この場合は、式2となる。

式2

　すなわち、解が複数（2個）存在する。このように、機構が複雑になると逆問題は解が複数となり、解の導出には工夫が必要となる。

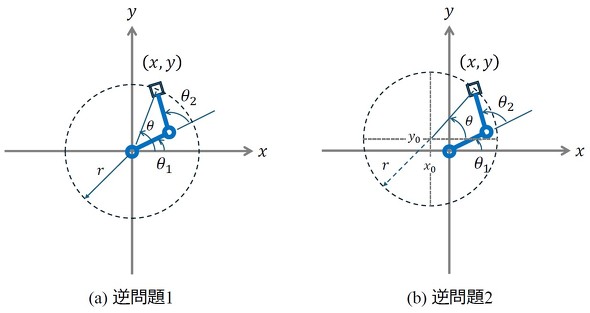
　回転2関節機構の逆運動学を図5に示す2つの事例で考える。

図5　逆問題の事例［クリックで拡大］

　最初に、図5（a）に示す逆問題1を考える。機構の先端（x，y）が半径rの円軌道上を角速度ωで一定回転するためには、各関節の角度をどのように変化させたらいいかという問題である。図5（a）より、以下の式が導出される（式3）。なお、以降、2つのリンクの長さは同じLとする。

式3

　上式を理論的に解いてもよいが、Modelicaでテキスト表記すると以下となる（リスト2）。ここではL＝2、r＝3とする。

model staticReverse1

import Modelica.Constants.pi;

Real theta;

Real theta1(start = pi/4);

Real theta2(start = -pi/2);

Real x;

Real y;

parameter Real L = 2;

parameter Real r = 3;

parameter Real omg = 2*pi;

equation

x = L*cos(theta1) + L*cos(theta1 + theta2);

y = L*sin(theta1) + L*sin(theta1 + theta2);

x = r*cos(theta);

y = r*sin(theta);

theta = omg*time;

end staticReverse1;

リスト2　Modelicaでテキスト表現

　リスト2を解けば解が求まるが、2リンク機構の逆問題の解は2個あることを既に述べた。Modelicaは自動的にこの2つの解を求めてくれるわけではないので、解の値をある程度予測して、初期値（θ₁，θ₂）を与えてあげる必要がある。

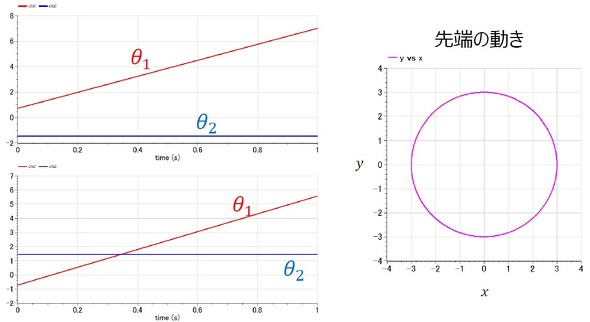
　リスト2の赤字部分が初期値に相当する。こうして求めた図5（a）の逆運動学の2つの解を図6に示す。このように、初期値によって異なる解にたどり着く。その際、解がいくつあるかを事前に知っておくことが重要である。図6からこの事例では第2関節の角度は一定値で、第1関節が一定角速度で動いていることが分かる。

図6　運動学逆問題1の解析例［クリックで拡大］

　次に、図5（b）に示す逆問題2を考える。機構の先端（x，y）が（x₀，y₀）を中心とした半径rの円軌道上を角速度ωで一定回転するためには、各関節の角度をどのように変化させたらいいかという問題である。図5（b）より、以下の式が導出できる（式4）。

式4

　上式をModelicaでテキスト表記すると以下となる（リスト3）。ここではL＝2、r＝2、x₀＝1、y₀＝1とする。

model staticReverse2

import Modelica.Constants.pi;

Real theta;

Real theta1(start = -pi/4);

Real theta2(start = pi/4);

Real x;

Real y;

Real X;

Real Y;

parameter Real L = 2;

parameter Real r = 2;

parameter Real omg = 2*pi;

parameter Real x0=1;

parameter Real y0=1;

equation

x = L*cos(theta1) + L*cos(theta1 + theta2);

y = L*sin(theta1) + L*sin(theta1 + theta2);

X=x-x0;

Y=y-y0;

X = r*cos(theta);

Y = r*sin(theta);

theta = omg*time;

end staticReverse2;

リスト3　Modelicaでテキスト表現

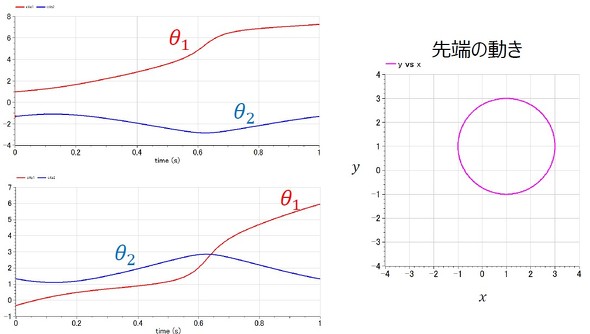
　リスト3を逆問題1と同様にして解くと、逆運動学の解は図7に示す2つの解となる。逆問題1と比べると各関節は複雑な動きをしており、第1関節だけでなく、第2関節も時間とともに変動している。

図7　運動学逆問題2の解析例［クリックで拡大］