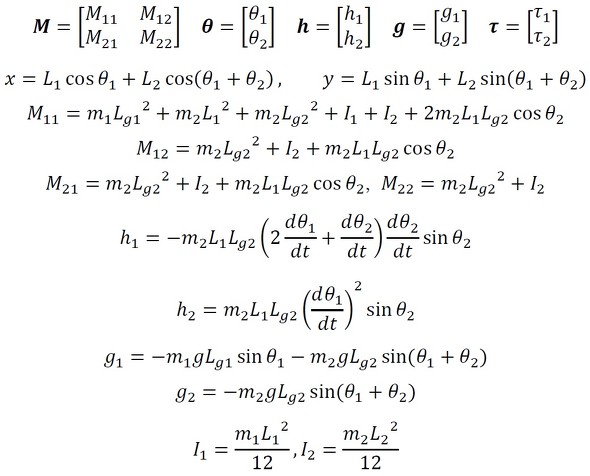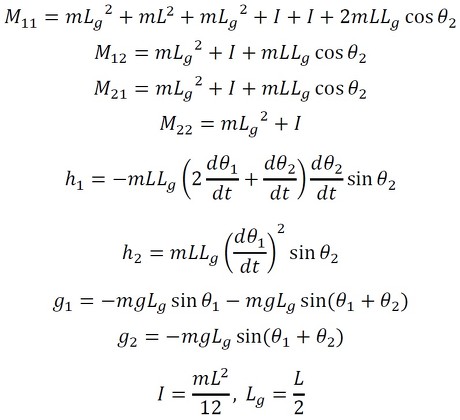機構制御系のモデリング（その3） 〜回転2関節機構の運動学・動力学を考える〜：1Dモデリングの勘所（38）（3/5 ページ）

「1Dモデリング」に関する連載。連載第38回では「機構制御系のモデリング（その3）」と題し、回転2関節機構の運動学、動力学を考えるについて考える。

[大富浩一／日本機械学会 設計研究会，MONOist]

動力学（運動方程式の導出）

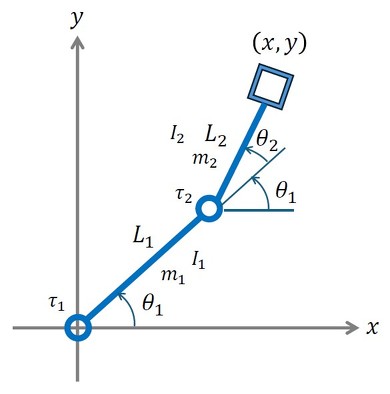
　図8に示す回転2関節機構の動力学について考える。

図8　回転2関節機構（動力学）［クリックで拡大］

　動力学の場合、運動学に加えて、運動体の慣性力を考慮する必要がある。そこで、各リンクの質量、回転慣性を考慮して運動方程式を導出する。運動方程式の導出は「ラグランジュの方程式」を用いると便利である。ラグランジュの方程式については次回説明する。ここでは、最終的に導出された運動方程式を以下に記す。

式5

式6

　上式でL_gはリンクの重心位置である。

　上式について、2つのリンクは同じ長さL、質量m、回転慣性Iであるとすると、以下の式のように簡略化できる（式7）。以降の解析ではこの式を用いる。

式7

動力学（順問題）

　回転2関節機構の運動方程式を用いて、順運動学をModelicaで解くことにする。ここでは、各関節の角変位（θ₁，θ₂）を一定の角度で動かしたときの、機構先端の動きと各関節に与える必要トルクを求める。各関節は1秒間で1回転するものとする。また、リンクの長さはL＝2、質量はm＝1とする。以上をModelicaで表記すると以下となる（リスト4）。

model dynamicJun

import Modelica.Constants.pi;

import Modelica.Constants.g_n;

Real theta1;

Real theta2;

Real theta1v;

Real theta1a;

Real theta2v;

Real theta2a;

Real tau1;

Real tau2;

Real h1;

Real h2;

Real g1;

Real g2;

Real x;

Real y;

Real Lg;

Real M11;

Real M12;

Real M21;

Real M22;

Real In;

parameter Real L = 2;

parameter Real m = 1;

parameter Real omg1 = 2*pi;

parameter Real omg2 = 2*pi;

equation

theta1v = der(theta1);

theta1a = der(theta1v);

theta2v = der(theta1);

theta2a = der(theta2v);

Lg = L/2;

In = m*L^2/12;

M11*theta1a + M12*theta2a + h1 + g1 = tau1;

M21*theta1a + M22*theta2a + h2 + g2 = tau2;

M11 = m*Lg^2 + m*L^2 + m*Lg^2 + In + In + 2*m*L*Lg*cos(theta2);

M12 = m*Lg^2 + In + m*L*Lg*cos(theta2);

M21 = m*Lg^2 + In + m*L*Lg*cos(theta2);

M22 = m*Lg^2 + In;

h1 = -m*L*Lg*(2*theta1v + theta2v)*theta2v*sin(theta2);

h2 = m*L*Lg*theta1v^2*sin(theta2);

g1 = -m*g_n*Lg*sin(theta1)-m*g_n*L*sin(theta1)-m*g_n*Lg*sin(theta1+theta2);

g2 = -m*g_n*Lg*sin(theta1+theta2);

x = L*cos(theta1) + L*cos(theta1 + theta2);

y = L*sin(theta1) + L*sin(theta1 + theta2);

theta1 = omg1*time;

theta2 = omg2*time;

end dynamicJun;

リスト4　Modelicaでテキスト表現

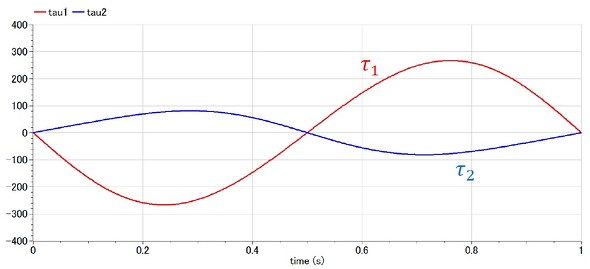
　リスト4を解析した結果（各関節の必要トルク）を図9に示す。なお、機構の動きは図3の運動学の順問題の結果と同じである。

図9　動力学順問題（解析例）［クリックで拡大］