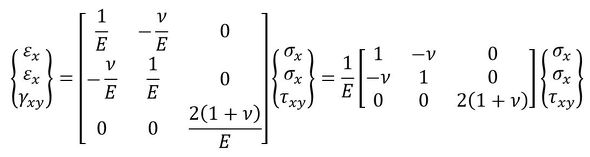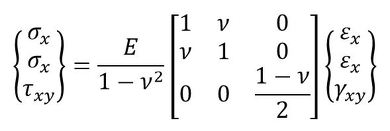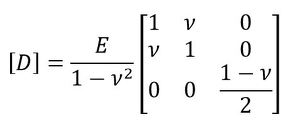有限要素法入門 〜連立方程式の解法、変位の計算〜:CAEを正しく使い疲労強度計算と有機的につなげる(3)(5/7 ページ)
金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第3回では、前回作成した全体剛性マトリクスから弾性変形後の変位を求める。そして、変位−ひずみマトリクス[B]を導出する。
応力−ひずみマトリクス[D]
応力−ひずみマトリクス[D]を求めましょう。応力−ひずみマトリクスは、ひずみベクトルを応力ベクトルに変換する行列です。次式で表されます。応力−ひずみマトリクス[D]は3行3列の行列となります。
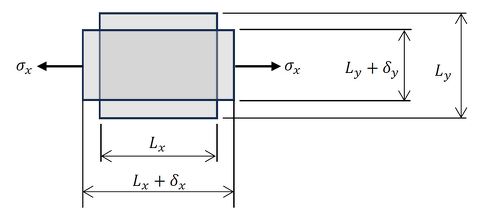
ポアソン比の定義を思い出しましょう。2次元平面応力問題として説明します。図6の通り、小さな四角形に対してx方向にσxの応力が作用しているとします。x方向にはδxだけ伸びて、y方向は応力が作用していませんがδyだけ縮みます。Ly+δyと表記したのでδyはマイナス値です。
ひずみは次式で定義されています。
体積保存則が成立していたらδyは自動的に決まりますが、金属などの弾性体は少し体積が増えます。δyは実験で求める必要があります。体積が増える度合いはポアソン比で表現できて、ポアソン比νは次式で定義されます。体積保存則が成立していたらν=0.5[-]となります。
σxとεxの関係はヤング率の定義から次式ですね。
ポアソン比を使うと、y方向ひずみは次式で表されます。
y方向にσyの応力が作用したときのx方向ひずみは上式と同様の考え方で次式となります。
x方向とy方向に同時に応力が作用したときのx方向ひずみは、式41と式43の和なので次式で表されます。
y方向ひずみは同様の考え方で次式となります。
せん断ひずみとせん断応力の関係は、せん断弾性係数Gの定義から次式となります。せん断弾性係数Gは、ポアソン比を使うとヤング率で表されることも考慮します。
式44、式45、式47を合体しマトリクス表示しましょう。
式47の逆行列を求めればよいのですが、それよりも式44、式45の連立方程式を解いた方が楽ですね。応力ベクトルは次式で求まります。
応力−ひずみマトリクス[D]は次式となります。
式の数が50個近くにもなってしまいましたね。キリが良いので今回はこの辺にしますが、少し寄り道をしましょう
Copyright © ITmedia, Inc. All Rights Reserved.