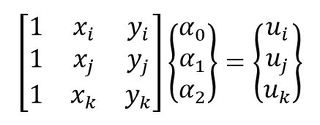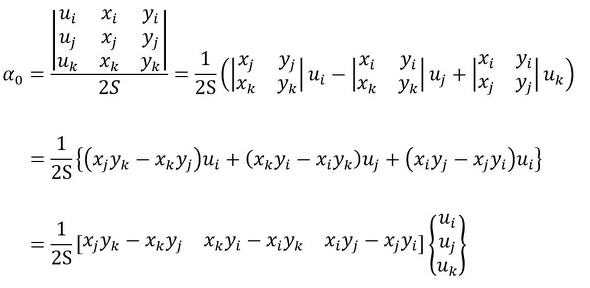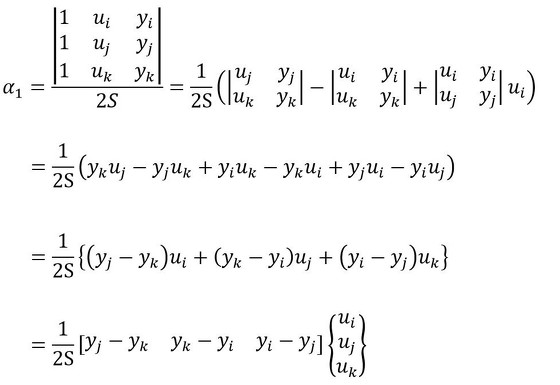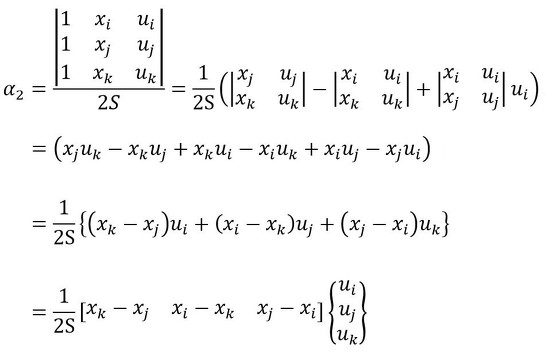有限要素法入門 〜連立方程式の解法、変位の計算〜：CAEを正しく使い疲労強度計算と有機的につなげる（3）（3/7 ページ）

金属疲労を起こした際にかかる対策コストは膨大なものになる。連載「CAEを正しく使い疲労強度計算と有機的につなげる」では、CAEを正しく使いこなし、その解析結果から疲労破壊の有無を予測するアプローチを解説する。連載第3回では、前回作成した全体剛性マトリクスから弾性変形後の変位を求める。そして、変位−ひずみマトリクス［B］を導出する。

[高橋良一／ＲＴデザインラボ 代表，MONOist]

要素内部の変位を式で表そう

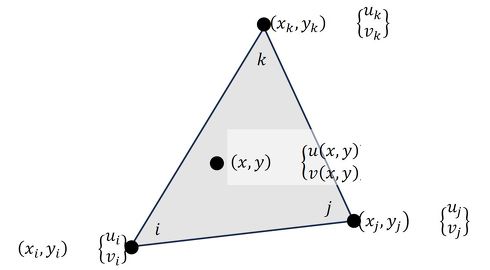
　図5に示した要素内部の任意の点（x，y）の変位を求める式を作りましょう。この式が有限要素法の解析精度を決定づけます。

図5　要素の節点座標と変位［クリックで拡大］

　手掛かりとなる情報は以下の6つです。

• i節点において、つまり座標（x_i，y_i）において、x方向変位はu_iである
• i節点において、つまり座標（x_i，y_i）において、y方向変位はv_iである
• j節点において、つまり座標（x_j，y_j）において、x方向変位はu_jである
• j節点において、つまり座標（x_j，y_j）において、y方向変位はv_jである
• k節点において、つまり座標（x_k，y_k）において、x方向変位はu_kである
• k節点において、つまり座標（x_k，y_k）において、y方向変位はv_kである

　要素内部の任意の点（x，y）の変位を求める式を次式としましょう。

式24

式25

　先に答えを言っておくと、式24と式25はx，yの1次式です。よって、このような要素を「1次要素」といいます。未知数はα₀，α₁，α₂，β₀，β₁，β₂と6個、手掛かりとなる情報も6個です。連立方程式を解けば式24、式25が作れそうです。連立方程式は以下となります。

式26-1

式26-2

式26-3

式26-4

式26-5

式26-6

　3元連立方程式が2セットになりました。式26-1、式26-2、式26-3をマトリクス表示すると次式となります。

式27

　行列式を使った連立方程式を求める方法を使います。未知数は次式となります。

式28

式29

式30

式31

　β₀，β₁，β₂も同じ方法で求まりますね。