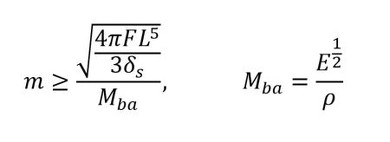物性を起点としたモデリングについて考える：1Dモデリングの勘所（17）（2/4 ページ）

「1Dモデリング」に関する連載。連載第17回は「物性を起点としたモデリング」をテーマに、まず物性について種々の視点から考察し、これを受けて物性を起点とした材料力学、熱力学、電気、感性とモデリングの関係について考える。

[大富浩一／日本機械学会 設計研究会，MONOist]

材料力学とモデリング

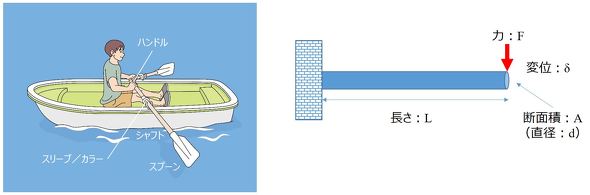
　材料力学とモデリングを、図4に示すボートのオールの設計問題（参考文献［1］）を通して考える。

図4　ボートのオールの設計問題［クリックで拡大］

　ここで知りたいのは「ボートのオールの材料として何を選定すべきか？」ということである。設計問題であるため、この問題を以下のように定義する。

• 設計目標：軽くて剛なオール
• 制約条件：長さ、曲げ剛性、破壊靭性
• 目的変数：質量の最小化
• 設計変数：シャフト径、材料

　オールは図4右図に示すように、長さL、断面形状は直径dの円形で、断面積はA、力Fを加えた際の変位（たわみ）をδとする。

　“軽い”とは“質量が小さい”ことであるため、オールの質量

式1

が目的関数となる。ρ［kg/m³］は材料の密度である。長さLは制約条件として、断面積A（直径d）は自由に変えられるものとする。

　一方、“剛な”梁（はり）とは“変位（たわみ）が小さい”ことを意味する。力Fを受ける片持ち梁の変位は材料力学の式より、δ＝FL³／3EIとなり、I＝πd⁴／64なので、δ＝64FL³／3πEd⁴となる。これが目標値の変位δ_sよりも小さい必要があるため、64FL³／3πEd⁴≤δ_sが制約条件となる。この式を変形して、

式2

が得られる。式1と式2からA（d²）を消去して、

式3

となる。すなわち、M_baの値が大きいほど“軽くて剛な梁”となる。

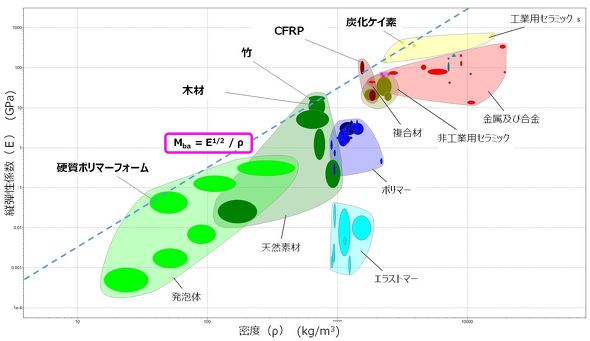
　図5にさまざまな材料について、縦軸に縦弾性係数、横軸に密度をとり、M_baが最大となる線を描いている（縦軸、横軸を対数表示することにより、M_ba一定の線は傾き2の直線で表現される）。これにより、軽くて剛な材料として、炭化ケイ素、CFRP、竹、木材、硬質ポリマーフォームが候補となる。このように物性を起点としたモデルを設計問題に適用することにより、最終的に材料の選定問題に帰結する。図5のように、縦軸横軸に物性およびこれからなる式をとり、さまざまな材料をプロットした図を「Ashbyマップ」（参考文献［1］）と呼ぶ。

図5　ボートのオールの材料選定［クリックで拡大］

参考文献：

• ［1］M. F. Ashby, Materials：Engineering, Science, Processing and Design, 4th edition, Butterworth-Heinemann（2018）