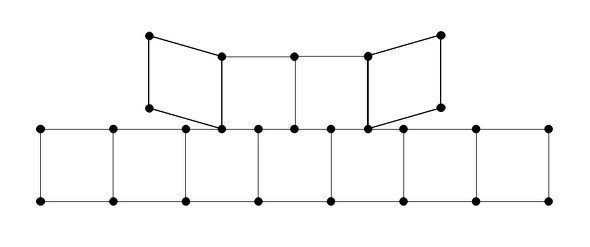
境界条件非線形性をもたらす接触と追従荷重について理解する：いまさら聞けない 非線形構造解析入門（5）（2/4 ページ）

多くの3D CADではオプションとしてCAE機能が用意されているが、多くの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。連載第5回では、3つの非線形性のうちの最後の1つ「境界条件非線形性」について取り上げる。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

ラグランジュ未定乗数法

　ラグランジュ未定乗数法自体は、ある拘束条件下における最適化を行うための手法ですが、いくつかの関数の値を拘束した上で、別の関数の極値を求めるものです。こちらに関しての数学的な説明は、ネット上にも分かりやすい解説などがありますので、それらをご参照いただければと思います。

　ラグランジュ未定乗数法とは、ごくごく簡単に言うと、2つのボディが接触した際に接触面上に「接触力」という未知数（自由度）を導入して一緒に解く手法になります。この手法で解析を行う場合には、後で示すペナルティ法のような接触ボディ間の貫通が起きないため、相対的に精度の高い解析を実行できます。ただ、その一方で、この問題を解く際の離散方程式の対角項にゼロが入ってくることで非正定マトリクスが発生し、計算が不安定になることがあります。接触が絡む問題は大規模なものも少なくありませんが、大規模問題に多用される反復ソルバーなどには不向きな手法ともいえます。

図1　ラグランジュ未定乗数法。物体間の食い込みは発生しない［クリックで拡大］

ペナルティ法

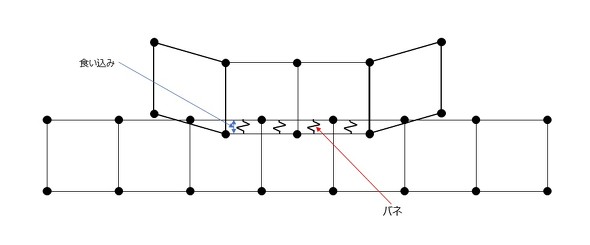
　ペナルティ法は、“ペナルティ”という言葉が「罰則」の意味で使われることからも分かる通り、ある拘束条件下において、その条件を破った時に“罰を与える”という考え方になります。接触解析の場合には、接触面において貫通が発生すると（物理的にはありえませんが）、貫通した量に応じて接触力を与えます。具体的には、接触面に仮想的なバネを生成し、その剛性で接触面における釣り合いを取っていくことになります。従って、貫通を許さないラグランジュ未定乗数法と比較すると、解に対する厳密性という観点からはデメリットがあるともいえますが、その一方で、安定して計算を進められるというメリットもあります。

図2　ペナルティ法。バネ剛性により釣り合いを取るがその性質上、微妙な食い込みが発生する［クリックで拡大］

拡張ラグランジュ法

　解析ソフトによっては、拡張ラグランジュ法（Augmented Lagrange法）という形で実装されていることが多いと思いますが、拡張ラグランジュ法はペナルティ法を強化したものといえます。こちらも接触面において、仮想的なバネを使って接触面上の釣り合いを表現しますが、ペナルティ法の安定性のメリットを維持しつつ、計算の収束性の改善を図った実装がなされています。

　解析ソフトの種類にもよりますが、複数の接触手法を選択できることも少なくありません。例えば、当初デフォルトの接触条件で解析を進めつつも収束性が悪く解析中に問題が発生した場合や、解析の種類によっては、手法を切り替えることはよくあります。もっともヘルプなどを見ても、そのオプションの特徴に関する記載はあっても、実装の基となる理論についての記述がないことがほとんどだと思いますが、商用ソフトを使用する場合にはそれでも特に問題はありません。

　一般的には「Node to Surface（節点と面）」または「Surface to Surface（面と面）」という選択肢が用意されていると思います（ただし、場合によっては使えないオプションもある）。そのあたりは、使用している解析ソフトのマニュアルやヘルプなどをご覧ください。