材料非線形性の基礎、そして複雑な材料モデルの理論を知る：いまさら聞けない 非線形構造解析入門（4）（3/4 ページ）

多くの3D CADではオプションとしてCAE機能が用意されているが、多くの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。連載第4回では、3つの非線形性のうちの1つ「材料非線形性」について取り上げる。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

超弾性材料

　昨今の工業製品は、金属だけでなく樹脂やゴムなどの高分子材料の使用頻度も増えています。ABSをはじめとして、いわゆるエンジニアリングプラスチックなどの樹脂は、金属に準じた挙動を想定した材料物性の定義で、十分に妥当な挙動をシミュレーションの結果として得ることができます。

　しかし、ゴムなどのような柔軟性に富み、かつ非常に大きな変形をする材料の場合には、ヤング率とポアソン比などで物性値を表現することがあまり適切ではなく、別の形式での定義が必要となってきます。そこで、一般的に「超弾性」と呼ばれる物性値の表現形式が導入されることになります。

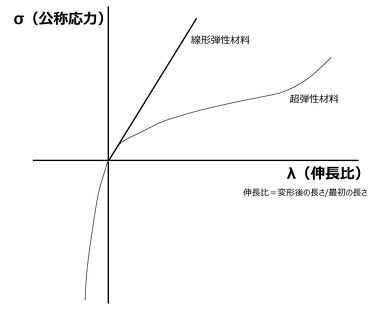
　なぜ、そのような定義が必要なのかということですが、以下の弾性材料と超弾性材料の比較を見てみましょう。

図7　超弾性材料と線形弾性材料の比較［クリックで拡大］

　ひずみの領域が非常に微小な場合は、それほど大きな差はないのですが、ひずみのレンジが大きくなればなるほど異なる挙動であることが分かります。また、弾性材料とは違って超弾性材料は、応力・ひずみ曲線が直線ではなくS字のような曲線を描いていることも分かります。つまり、弾性材料でゴムの挙動を表すのが難しいことを意味しています。

　さて、かなり長い話となりますので詳細は省きますが、超弾性材料をどのように表すのかについて紹介したいと思います。

　超弾性の材料は、「ひずみエネルギー（W）」を示す関数で表現します。そして、実はこのひずみエネルギーの表現方法は複数あるため、ゴムを表現するための材料モデルも複数存在します。その例を以下に示します。

• Neo-Hookean（ネオフッキアン）

式1

• Mooney-Rivlin（ムーニー・リブリン）

式2

• Ogden（オグデン）

式3

　上記の式の中で、C₀₁やC₁₀として表現されているものが材料物性の定数であり、弾性材料でいえばヤング率などに相当するものです。Iは「ひずみの不変量」と呼ばれるもので、式3のオグデンの式の中にあるλは、伸長比の各成分になります。

　これらの材料に使用される定数の取得方法ですが、基本的には材料の試験によります。試験から応力と伸長比のデータポイントを得て、それらのデータポイントから定数を取得します。具体的には、各ポイントのデータに対してカーブフィットを行って取得していきます。

　従って、ゴム材料の定義において、あらかじめC₁₀などの値が分かっていない場合には、解析プログラムとは別に、カーブフィッティングを行うプログラムも必要になります。ただし、解析ソフト（プリポスト）によっては、カーブフィッティングのプログラムを組み込んでいるものもあります。

　材料の試験ですが、一般的には連続体力学の変形モードに沿って、「単軸引張り」「等二軸引張り」「単純せん断」の3つの試験が必要とされます。ただし、単純せん断試験は実施が困難であるため、平面せん断試験に置き換えることが一般的だと思います。

　これら3つのモードを適切に考慮した材料物性の定義を行わないと、場合によっては不正確どころか、「これはあり得ない……」というような変形がシミュレーションの結果として得られることがあります。