材料非線形性の基礎、そして複雑な材料モデルの理論を知る：いまさら聞けない 非線形構造解析入門（4）（2/4 ページ）

多くの3D CADではオプションとしてCAE機能が用意されているが、多くの方が「線形解析」での利用にとどまっており、「非線形解析」にまで踏み出せていない現状がある。本連載では、構造解析でも特に非線形解析にフォーカスし、初心者向けに分かりやすくその特長や活用メリットなどを紹介する。連載第4回では、3つの非線形性のうちの1つ「材料非線形性」について取り上げる。

[水野操 mfabrica合同会社 社長／3D-GAN，MONOist]

弾塑性材料を使った解析における物性値や設定について

　まず、項目のみ列挙してみました。以降でこれらの詳細について解説していきます。なお、弾塑性を語る上では「流れ則」というものもありますが、商用ソフトを使用する上では直接扱うことはないので、ここでは割愛します。

• ヤング率
• ポアソン比
• 降伏応力
• 塑性領域における（降伏後の）応力とひずみの関係
• 降伏条件
• 硬化則

ヤング率とポアソン比

　ヤング率とポアソン比については、先ほどから述べている通り、線形弾性解析でも用いる値で、皆さんもおなじみの物性値だと思いますので、ここでの説明は簡単にさらっと流します。ヤング率は「縦弾性係数」ともいい、フックの法則が成立する弾性域において、同軸方向の応力とひずみを関連付ける定数のことです。この数値が大きいほど剛性が高く、小さいほど剛性が低いということで、材料の剛性を見るのに分かりやすい指標といえます。

　私たちがよく用いる材料のうち、例えば、合金鋼であれば21万MPa、アルミ合金であれば7万MPaあたりが一般的だと思います。この値は材料に固有の値となります。

　次に、ポアソン比ですが、これはある物体を引っ張って応力が発生する状態にしたとき、その方向に沿って発生するひずみと、その方向に対して直交する方向に発生するひずみの比のことをいいます。私たちがよく使用する金属材料であれば、0.3前後のものが多いのではないでしょうか。ゴムのような非圧縮材料の場合には、0.49など限りなく0.5に近い値になります。

　弾塑性材料も塑性するまでは弾性挙動を示すわけなので、弾性解析と同様にこの2つの値は必要です。

降伏応力

　降伏応力は、線形弾性解析であれば、計算そのものには必要のない値です（ポスト処理などで安全率の算定には用いられますが）。しかし、弾塑性解析の場合には、この応力を超えた時点で材料の挙動が変わるので、重要な値となります。

　ところで、解析で用いる応力テンソルには9つの値がありますが、どの応力を降伏応力と比較するのでしょうか。降伏応力という1つの値と比較するので、テンソルのままでは都合がよくありません。

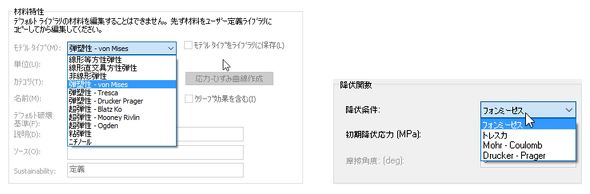
　そこで、相当値と比較する必要があるのですが、実はその相当値についてはいろいろな理論があり、使用する材料などによって適切なものを用いる必要があります。使用頻度が最も多い金属の材料では、「von Mises（フォン・ミーゼス）型」を利用するのが一般的で、設計者CAEなどでも降伏の判定にミーゼス型がデフォルトでよく用いられます。その他のものとして、「トレスカ」や「モール・クーロン」などがよく知られていると思います。トレスカの降伏条件は、材料の最大せん断応力がある値に達すると降伏するという条件です。

図5　（左）「SOLIDWORKS Simulation」と（右）「Inventor Nastran」の降伏条件定義［クリックで拡大］

塑性領域における（降伏後の）応力とひずみの関係

　塑性域における応力とひずみの関係も別途定義が必要です。弾性域では応力とひずみはヤング率という定数で関係付けられましたが、塑性域ではそのような単純な関係ではないため、試験を行って得られたデータポイントとそれらデータポイントの線分で補間された形で表現されることが多いのではないかと思います。

　また、この定義に使用する応力とひずみも、一般的な「公称応力」と「工学ひずみ」ではなくて、「真応力（コーシー応力）」と「真ひずみ（対数ひずみ）」で定義することが必要な場合もあります。定義方法については、ご自身が使用するソフトのマニュアルなどに従ってください。

硬化則

　金属などの材料が降伏し、さらに続けて載荷された場合には塑性域の応力・ひずみ曲線に沿って変形が進みます。そして、ある程度まで永久変形が進んだ状態で除荷して、載荷している荷重値をゼロにします。その上で、再度塑性するまで載荷するとします。その場合、実は塑性は最初の降伏応力（初期降伏応力）では塑性しないで、前回除荷したときの応力まで弾性挙動が続き、その後に降伏します。つまり、この物体は“硬化していた”ということになります。そして、その材料がどのように硬化するのかを定義したものを「硬化則」といいます。

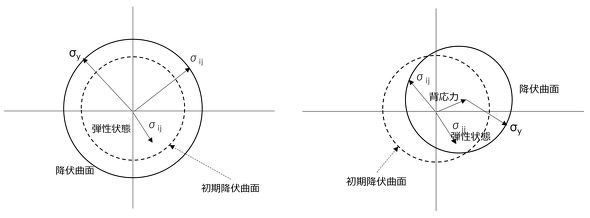
　主に使用される硬化則としては、「等方硬化則」「移動硬化則」「混合（複合）硬化則」の3つがあります。弾塑性解析が可能なソフトであれば、これらの3つの硬化則が組み込まれていることが多いと思います。どの硬化則を使うのかは、どのような塑性加工がされるのかに依存してきます。なお、図6に「降伏曲面」というものがありますが、降伏関数に基づいて材料が塑性している間、応力はこの曲面の上を移動します。弾性状態の場合には、応力はこれらの円の内側にあります。

図6　（左）等方硬化則と（右）移動硬化則［クリックで拡大］

　一般的な塑性加工であれば等方硬化則を使用することが多いと思いますが、繰り返し硬化などの場合には等方硬化則は不適切で、移動硬化則が推奨されます。複合硬化則は、等方硬化則と移動硬化則を併せ持ったものになります。

　ただ、繰り返し硬化則は一般に複雑で専門的な解析になる場合もあり、ここで紹介したもの以外の硬化則を用いないと妥当な解が得られないことがあります。そういう意味では、複雑な繰り返し塑性を伴う塑性解析は、よりこの分野の専門家向けの解析といえるかもしれません。