EVのモデリングを「ミニ四駆」で考える〜バッテリー、モーター、走行の連成問題、現象を本質的に捉えてシンプルに表現〜：1Dモデリングの勘所（10）（3/4 ページ）

「1Dモデリング」に関する連載。前回行った「ミニ四駆」の構成要素の原理理解、定式化を受けて、今回はミニ四駆全体系のモデリングを行い、解析を実行する。さらに現象を理解する方法としてモデリング結果を図で表現することの有用性に触れる。最後に、「Modelica」によるミニ四駆のモデリング例を示す。

[大富浩一／日本機械学会 設計研究会，MONOist]

解析結果と考察

　図1の5つの式を基に未知数、パラメータ、方程式をModelicaで直に書くと以下となる。ここに、g_nは重力加速度を意味する。

model mini4Drive
 import Modelica.Constants.g_n;
 Real Tm;
 Real I;
 Real Om;
 Real Ft;
 Real v;
 parameter Real Rm=1;
 parameter Real Rb=0.8;
 parameter Real E=3;
 parameter Real Ke=1.2e-3;
 parameter Real Kt=1.2e-3;
 parameter Real Gr=5;
 parameter Real Ita=0.6561;
 parameter Real r=0.015;
 parameter Real Mu=0.1;
 parameter Real m=0.1;
 parameter Real Cd=0.3;
 parameter Real A=0.004;
 parameter Real Ro=1.205;
equation
 Tm=Kt*I;
 Om=(E/Ke)-(Rm+Rb)*Tm/(Ke*Kt);
 Ft=Gr*Tm*Ita/r;
 v=Om*r/Gr;
 Ft=Mu*m*g_n+(1/2)*Cd*A*Ro*v^2;
end mini4Drive;

　上式を解くと、

• けん引力：F_t＝0.120［N］
• 電流：I＝0.456［A］
• モーター回転数：ω_M＝1817［rad/s］＝17349［rpm］
• モータートルク：T_M＝0.000547［Nm］
• 速度：v＝5.45［m/s］＝19.6［km/h］

という結果が得られる。ここで、バッテリーの容量を1Whとすると、走行時間は、

式12

となり、走行距離は、

式13

となる。

現象の理解

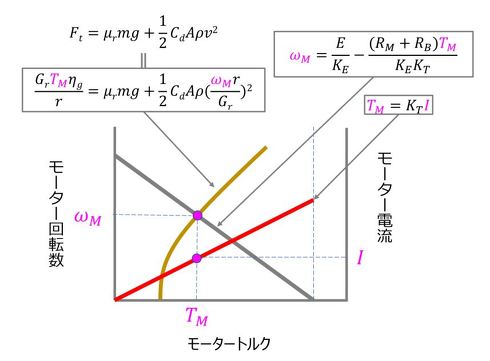
　以上、現象の理解を方程式で表現することで行った。これはこれで重要なことであるが、できれば図として現象を直感的に理解できると役に立つ。ミニ四駆の主要要素はバッテリー、モーター、走行系であり、この3つの要素を支配する現象を1つの図に表現することを試みる。モーターは既に述べたように、回転数ω_MとトルクT_Mの関係式で表現できる。バッテリー電流はトルク定数を介して、モータートルクにひも付けられる。一方、走行系は、

式14

で表現でき、この式に図4のF_tとvの定義式を代入すると次式が得られる。

式15

　以上のバッテリー、モーター、走行系に関する式を1つの図で表現すると図5となる。すなわち、モーターの式と走行系の式の交点がモーターの運転点（T_M、ω_M）で、このトルクT_Mと電流の式の交点が電流値Iとなる。

図5　現象の理解［クリックで拡大］

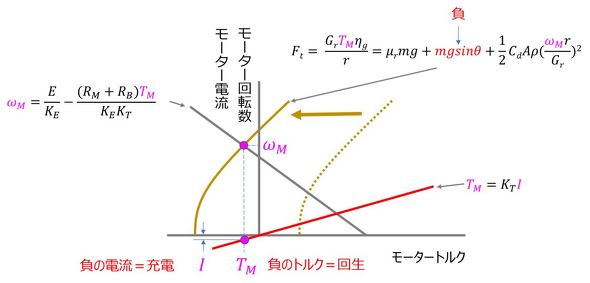
　図5の図表現による現象の理解の応用例として、急勾配の下り坂を走行している状況を考える。この場合、走行系の式は、

式16

となる。mgsinθは急勾配の下り坂を下る際の力で負の値となる。従って、急勾配の下り坂を下る際の走行系の式（二次曲線）は、図6に示すように左側に平行移動する。そうすると、負のトルク、負の電流が発生する。すなわち、バッテリーが充電状態となる。これを「回生」という。図6では分かりやすくするために、モーター特性は変わらないとしているが、実際には、回生制動（回生ブレーキ）により、走行中にモーターに制動トルクを発生させることで、図6に示すよりも大きな電気エネルギーを回収できる。

図6　急勾配の下り坂を走行時の状況（回生）［クリックで拡大］