CAEはメッシュが命!:構造解析、はじめの一歩(7)(1/3 ページ)
「構造解析」を“設計をより良いものとするための道具”として捉え、実践活用に向けた第一歩を踏み出そう。第7回は「有限要素法」の主役である“要素”にフォーカスし、有限要素の種類、次数、要素サイズが解析結果にどのような影響を与えるのか、テスト結果を交えてステップ・バイ・ステップで解説する。
※注意※
- ヤング率、ポアソン比など、基本的な材料力学の知識があることを前提としています。材料力学の知識を持たずして解析を行うことは、免許を持たずしてクルマの運転をするのと同じことです。「危険」であることを心得ておいてください
- ソフトウェアのインストールや使用については、自己責任ということでお願いします
- 今回の記事は、連載第5回の「線形静解析」で説明した部分が大幅に省略されています。ぜひそちら(連載第5回)の記事に目を通してからご覧ください
有限要素は解析品質をつかさどる
これまで、座学とCAEの必要性、設計者CAEのベースとなる3次元CADモデル、そして、設計者CAEの登竜門である「線形静解析」と「固有振動数解析」について解説してきました。
ここでどうしても話しておきたいことがあります。それは「有限要素」のことです。「有限要素法」という名の通り、有限要素法による解析は“要素が命”なのです。
設計者CAEで使う要素は次の一択です。それが結果であり、答えであり、レコメンドです。
設計者CAEでは、四面体の2次要素を使う
これさえ押さえておけば、問題ありません。どの要素を使えばいいかを、単なるノウハウとして知っていることも大切ですが、有限要素の種類や次数、サイズによってどれくらい解析結果が変わってしまうのか、“身をもって”知っておいてほしいのです。
解析で使用する要素の種類と次数、サイズは、解析の品質と精度を決める重要な要因の一つです。それはつまり、解析で思ったような精度が出ないときに問題を切り分けるための要因の一つでもあるということです。
さらに、要素の種類と次数、サイズによって、解析結果のミーゼス応力図が変わります。そのことを知らないと、応力の評価を間違えてしまいます。
設計者の皆さんは本当に忙しいので、有限要素の精度のチェックなどしているヒマはありません。ここでは、筆者が実際に有限要素のテストをしてみたいと思います。筆者の行う有限要素テストの結果を観察することで、皆さんなりの解釈や気付きが得られることでしょう。それこそが知識であり、ノウハウです。
使用するモデル
使用するモデルは、以前の筆者の連載で登場した「片持ちばり」とします。今回も要素の次数を変更して解析を行っています。
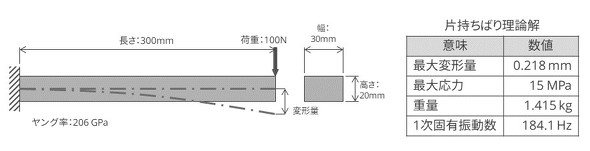
使用するモデルの寸法と理論解を図1に示します。この片持ちばりモデルと理論解をアタマの片隅に入れておくと、いろいろな面で役に立ちます。
要素の検証
それでは、要素、次数、サイズを変更しながら、線形静解析をやってみましょう。使用したソフトウェアはオートデスクの「Fusion 360」(バージョン:2.0.8816)です。
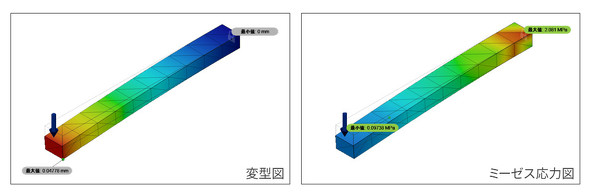
四面体1次要素/要素サイズ 30mm
最大変形量は0.0478mmです。これは理論解の22%程度です。
応力図を見てください。構造も荷重も拘束も対称なのですから、ミーゼス応力図も対称になるはずです。それなのに、対称になっていません。
理論解によると最大応力は15MPaですが、解析値は理論解の14%の2.08MPaです。有限要素法のクセを全く知らないと、この結果を盲信してしまうことになります。
四面体1次要素で、要素サイズ30mmの有限要素モデルは「全く使いモノにならない」という結果となりました。
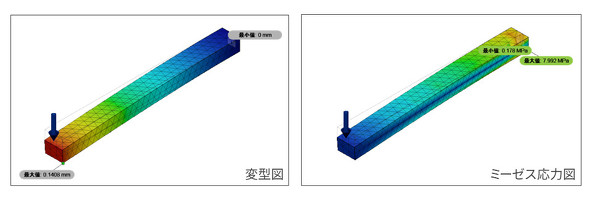
四面体1次要素/要素サイズ 10mm
要素サイズを一気に3分の1の10mmにしてみました。最大変形量は0.141mmです。要素サイズが30mmのときと比べると、グッと理論解に近づきましたが、それでも理論解の65%程度です。
ミーゼス応力図の応力分布はだいぶまともになりました。しかし、最大応力は8MPと計算されました。これは理論解の53%です。
要素サイズが10mmでも、使いモノにならないことが分かりました。
Copyright © ITmedia, Inc. All Rights Reserved.