位置公差の総仕上げと振れ公差について 〜曖昧さを取り除く幾何公差〜:産機設計者が解説「公差計算・公差解析」(15)(3/4 ページ)
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。最終回となる第15回は「位置公差」の残りと「振れ公差」について取り上げ、幾何公差の解説をまとめます。
3.振れ公差(Runout tolerance)
「振れ公差」とは、ある直線を回転の軸にして部品を回転させるとき、部品形体の振れの変動値を規制する幾何公差となります。振れ公差には、「円周振れ公差」と「全周振れ公差」の2つがあります。
「JIS B 1192:2013 ボールねじ」を見ると、
ねじ軸の支持部軸線に対するねじ溝面の半径方向の円周振れおよび部品取付部外径の半径方向の円周振れ
とあり、振れ公差が規格として表されています。
3−1.円周振れ(Circular runout)
円周振れについて、JISで確認してみると、
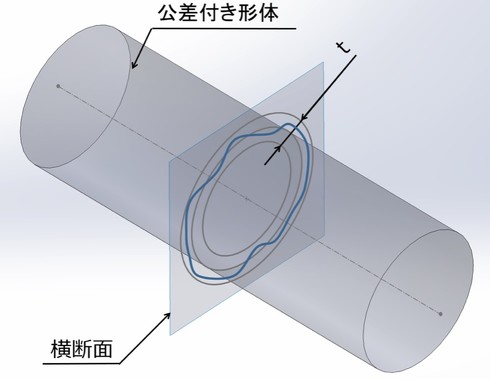
データム軸直線を軸とする回転面を持つべき対象物またはデータム軸直線に対して垂直な円形平面であるべき対象物をデータム軸直線の周りに回転したとき、その表面が指定した位置または任意の位置で指定した方向に変位する大きさをいう
と定義されています。簡単に言うと、円周振れ公差とは「回転する円筒表面上の一(いち)断面」に公差が適用される形体になります。
円周振れ公差については、
- 半径方向
- 一軸方向
- 任意の方向における円周振れ公差
- 指定方向における円周振れ公差
があります。ここでは、半径方向について説明します。
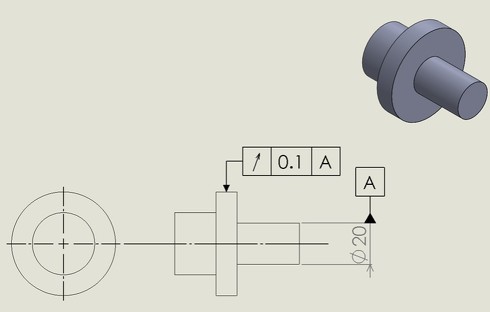
円周振れ:半径方向
JIS B 0021にも記載されていますが、通常「振れ」は軸の周りの完全回転に適用されますが、1回転の一部分に適用するために規制することが可能です。
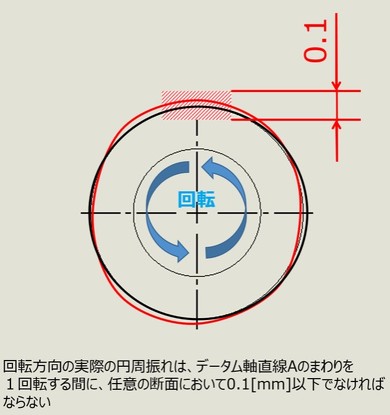
なお、円周振れは「任意の位置の円筒表面がデータム軸と同軸となる幅(図12、図13では0.1[mm])の2円間にある」ことを規定するものであり、この全ての面について規定するものではありません。
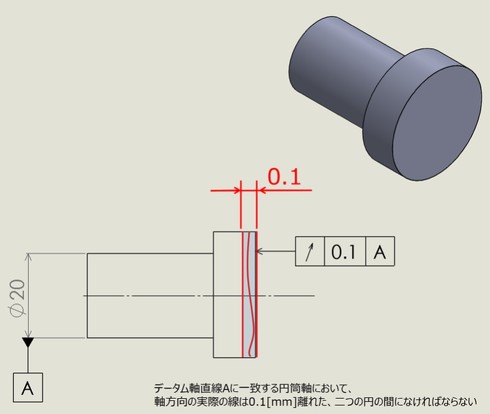
円周振れに関して、図12、図13では「ラジアル方向(回転軸に対して放射方向[Radial])」について示しましたが、「アキシャル方向(軸方向[Axial])」についてもあります。アキシャル方向の円周振れを使用した図面を以下に示します(図14)。
アキシャル方向の円周振れについても、「任意の位置の円筒端面がデータム軸と直角な幅(図14では0.1[mm])の2面間」について規定しており、この全ての面について規定するものではありません。
Copyright © ITmedia, Inc. All Rights Reserved.