データムを必要とする幾何公差【その5】～位置公差の位置度～：産機設計者が解説「公差計算・公差解析」（12）（3/4 ページ）

機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第12回は「位置公差」のうち「位置度」について取り上げる。

LINE

Hatena

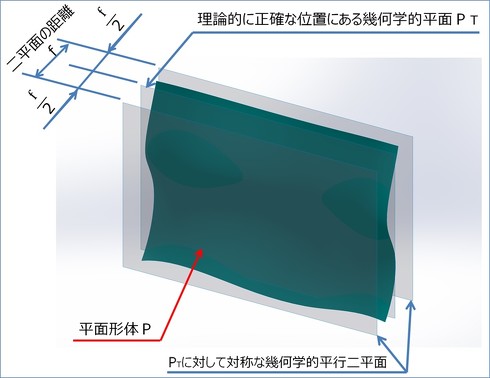
2－1－3．平面形体の位置度

公差域の定義（JIS原文から参照図番号を編集）
　平面形体の位置度は、理論的に正確な位置にある幾何学的平面（PT）に対して対称な幾何学的平行2平面でその平面形体（P）を挟んだときの、2平面の間隔（f）で表す。

図6　平面形体の位置度［クリックで拡大］

　以上、位置度の定義について説明しました。

　さらに、位置度公差方式として「JIS B 0025：1998 製図－幾何公差表示方式－位置度公差方式」によって、次のような適用範囲で、標準化されています。

　これまでの定義とともに、位置度公差方式について説明します。位置度公差方式とは、サイズ公差方式のように、サイズに公差を入れるのではなく、形体が理論的に正確な寸法により指示された位置に公差域を設定する方式です。

　例えば、規則的に配置された穴の場合、サイズ公差方式では公差の累積を考えなければなりませんが、位置度公差方式では、この公差の累積問題はなくなります。

　さて、最大実体公差方式についてご存じでしょうか。最大実体公差は、よく耳にする語句ですが、「その使用方法は簡単ではない」というのが筆者の印象です。実は、この位置度公差方式こそが、最大実体公差方式の基礎となる部分なのです。最大実体公差方式については、次回説明します。

　次に、位置度公差の使用例について説明します。まず、その手順です。

　ポイントとして、位置度公差方式は「サイズではなく位置の偏差（バラツキ）を規制する」ことから、データムが必須となるわけです。

　位置度公差方式を使用するメリットは、以下の通りです。

　位置度公差方式について、筆者は先輩から教わることもありませんでしたし、過去の図面の中で見ることもありませんでした。しかし、これらのメリットから非常に有効な方式だと理解しています。

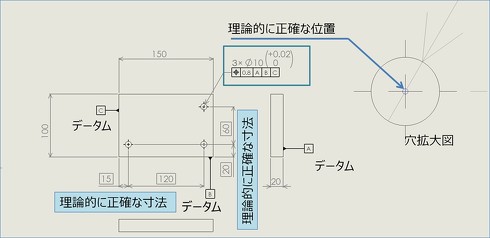
図7　位置度公差方式の記入例［クリックで拡大］

　この位置度公差方式の指示により、各穴の位置が以下のように規制されます。