データムを必要とする幾何公差【その2】〜姿勢公差の直角度〜：産機設計者が解説「公差計算・公差解析」（9）（3/4 ページ）

機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計／解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第9回はデータムを必要とする幾何公差をテーマに、姿勢公差の直角度について取り上げる。

[土橋美博／飯沼ゲージ製作所，MONOist]

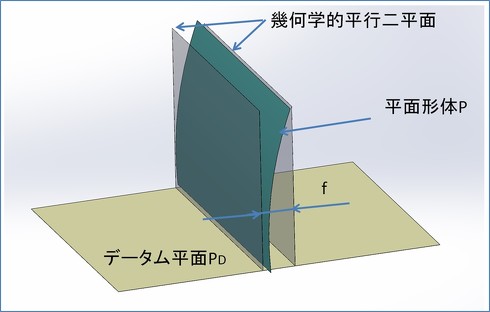
1−2−3．平面形体のデータム平面に対する直角度

・公差域の定義（JIS原文、以下同様）　
　データム平面（PD）に垂直な幾何学的平行2平面でその平面形体（P）を挟んだとき、平行2平面の間隔が最小となる場合の、2平面の間隔（f）で表す。

図8　平面形体のデータム平面に対する直角度。この直角度が表された図面はよく見るものでもあり、筆者もよく使用する

図9　平面形体のデータム平面に対する直角度の例。青色の平面形体は緑色のデータム平面形体に対して、直交する幾何学的平行2平面の距離0.1［mm］の領域に入っている必要があることを表している

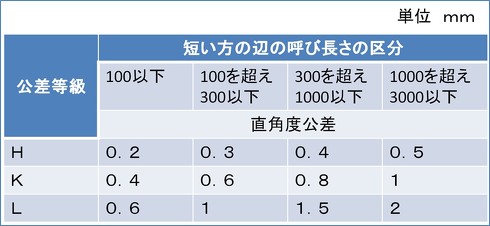
　この直角度公差は、頻繁に使用されます。このような公差は、個々に公差の指示を行わない場合も管理され、その適用はJISで定めるところであり、企業独自の公差値として管理されています。JISでは「JIS B 0419：1991 普通公差− 第2部：個々に公差の指示がない形体に対する幾何公差」として、その公差値が記載されています。

表1　JIS B0419−1991を参考に筆者作成

　公差等級は、H：精級、K：中級、L：粗級を表しています。この等級を見て、一体何を使用すればいいのか？　という疑問を持たれる方もいるかもしれません。これはあくまでも経験上の話ですが、筆者が所属する装置産業界における部品加工では、一般的な構造物を構成する部品として、中級を使用することがほとんどです。

　もちろん、部品の用途によっては精級を使用することもありますが、当然、加工コストも上がることになります。ただし、機能部品については、設計者が機能上必要な幾何公差値を設定します。また、企業の標準幾何公差として、何を使用するか定めていることが一般的でもあります。

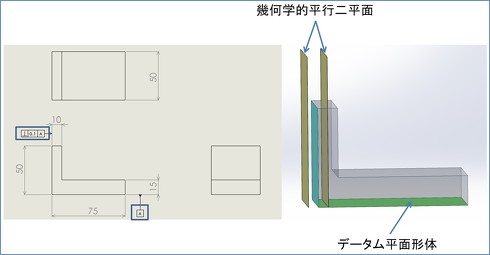
　この直角度の普通公差についてJISは、

直角を形成する2辺のうち長い方の辺をデータムとする。2つの辺が等しい呼び長さの場合には、いずれの辺をデータムとしてもよい

と規定しています。「直角度の普通公差のデータムとは何か」を再認識してみましょう。