コンピュータ・アーキテクトのためのモーター制御：SYSTEM DESIGN JOURNAL（2/5 ページ）

「モーターを制御する」。一見すると簡単な課題に思えますが、その原理や課題、現状を再確認すると、リアルタイムシステムアーキテクチャの今後の方向性を示していることが分かります。

[Ron Wilson，Altera Corporation. MONOist]

磁界方向制御

　問題は（オープンループ制御の常ですが）細部に潜んでいます。特に負荷がかかった状態でのモーター始動は、大ざっぱで著しく効率が低いことがあります。オープンループコントローラーは、負荷トルクまたは速度命令の変化に最適に応答せず、振動の抑制には全く役立ちません。よくある理由にもかかわらず、フィードバック制御システムの方がうまく機能するはずです。

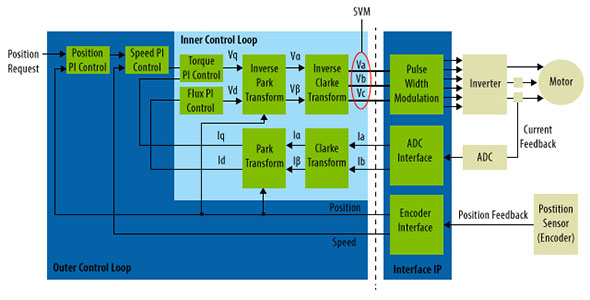
　要点は「何を制御するか」を把握することです。言うまでもなく、ロータ角度、あるいはアプリケーションによっては回転速度を制御しなければなりません。それには、回転磁界を発生させる、3つの巻線電流を制御する必要があります。業界では、磁界方向制御（FOC）と呼ばれる多段階プロセスがそのための最善の方法とされています（図2）。

図2.ドライブのブロック図

　まず、シャフトエンコーダからローター位置のサンプル、3つの巻線の2つから電流のサンプルを取得します。やや巧みな計算のおかげで、3つの巻線からの電流を全て取得する必要はありません。これらのサンプルから、ローターおよびステータの回転磁界の瞬時位置と遅れ速度が分かります。私たちの仕事は、回転磁界をローターの回転磁界より90度進んだ位置に維持しながら、ステータ巻線の電流振幅を制御することにより、ローターの速度または位置を制御することです。

　この仕事は、クラーク変換とパーク変換、2つの簡単な変換を使用すると簡単になります。クラーク変換は、120度離れた2つのスタータ巻線からの電流サンプルを直交ベクトル・ペアにマップします。ベクトルの方向はステータに対して固定であり、ベクトル和は当然ながら回転磁界ベクトルです。クラーク変換に必要なのは、電流値と定数を乗算し、積を累算する、つまり積和演算のみです。

　もう1つのパーク変換は、それら2つの直交ベクトルをロータの回転基準系にマップします。一方のベクトルはロータの磁界に一致し、もう一方のベクトル（直交ベクトル）はそれと直交します。パーク変換の方がやや難しく、瞬時シャフト位置を使用してsin（θ）およびcos（θ）係数を計算してから、ベクトル乗算を実行してベクトルをロータの基準系に変換します。

　ここで、制御可能な信号があります。ローターと一致する、つまりローターにトルクを加えていないスタータ磁束を表すベクトルは0に維持する必要があります。そこで、ステータ磁束が実際にトルクを加える直交成分を使用して、ロータの位置および速度を制御します。

　例えば、コントローラーは要求位置入力を受け取ると、通常の離散時間比例積分（PI）制御回路で実際のシャフト角度と比較し、FOCブロックに対して誤差信号出力を生成します。FOCブロックは、この誤差信号を直交トルク信号に変えてロータを回転させます。

　さらに逆パーク変換によってそのトルクを元のステータ巻線の固定基準系にマップし、逆クラーク変換によってトルク信号を電流にマップし、3つの巻線に加えます。このように、要求位置または要求速度入力の変化がスタータ巻線への信号を刺激してステータ磁界を回転させ、ロータを目的の角度に駆動します。

　全体の計算負荷はそれほどでもなく、FOCブロック内サンプル区間につき、2回の三角関数評価、10回の乗算、7回の加算に加え、PIコントローラーの実行に必要な2〜3回の演算ぐらいです。演算は少し気を付ければ全て固定小数点で行えます。現在の一般的な16kHzのサンプルレートとパルス幅変調速度は、32ビットMCUの整数性能からすれば大した負荷ではありません。しかし、処理はこれだけにとどまりません。