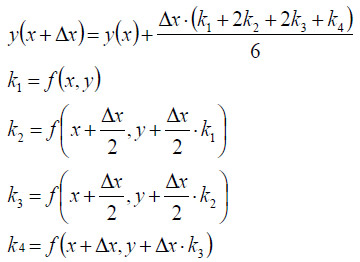オイラー法とルンゲ・クッタ法を使って微分方程式を解こう:無償ソフトで技術計算しよう【シミュレーション基礎編】(2)(2/2 ページ)
今回は、微分方程式を数値的に解く方法として、オイラー法とルンゲ・クッタ法について説明します。
ルンゲ・クッタ法
ルンゲ・クッタ法はオイラー法を改良したものです。ここでは、一般に用いられる4次のルンゲ・クッタ法について説明します。
ルンゲ・クッタ法ではオイラー法における式、
の代わりに、以下の式を用います。
他については同じです。
以上をFreeMatのプログラムにしたのが、ex402.mです。ex401.mのforループ内の式がルンゲ・クッタ法の式に変わった点以外は同じです。
clear;
f=inline('cos(x)');
x0=0;y0=0;xe=pi;n=11;
x=linspace(x0,xe,n);
y=zeros(1,n);
dx=(xe-x0)/(n-1);
y(1)=y0;
for k=2:n
k1=feval(f,x(k-1))*dx;
k2=feval(f,x(k-1)+dx/2)*dx;
k3=feval(f,x(k-1)+dx/2)*dx;
k4=feval(f,x(k-1)+dx)*dx;
y(k)=y(k-1)+(k1+2*k2+2*k3+k4)/6;
end
yy=sin(x);
plot(x,yy,'o-',x,y,'*-');grid('on');
title(['Division Number= ',num2str(n-1)]);
xlabel('x');ylabel('y');
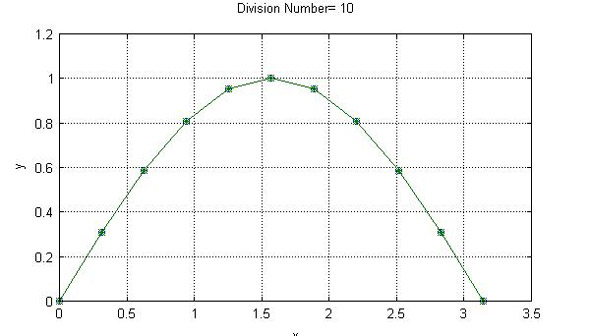
ex402.mで分割数を10にして計算してみた結果が図2です。
○で示す解析解と*で示す数値解とは良く一致していることが分かります。このように、ルンゲ・クッタ法は少ない分割数でも精度の良い計算ができるため、常微分方程式の数値解法の標準的な手法として広く使われています。もちろん、ルンゲ・クッタ法といえども万能ではなく、今回の例のような性質の良い(急激に変化しない)微分方程式以外にも対応できるような各種の方法が提唱されています。
微分方程式と条件を与えれば、解いてくれるような汎用的なプログラムがあれば、いちいちプログラムを作成せずに済むので便利です。そこで、ex402.mを関数と解析条件とを入力引数に持つ関数mファイルにしたのがrk4.mです。
function xy=rk4(func,x0,xe,n,y0)
f=inline(func);
x=linspace(x0,xe,n+1);
y=zeros(1,n+1);
dx=(xe-x0)/n;
y(1)=y0;
for k=2:n+1
k1=feval(f,x(k-1),y(k-1))*dx;
k2=feval(f,x(k-1)+dx/2,y(k-1)+k1/2)*dx;
k3=feval(f,x(k-1)+dx/2,y(k-1)+k2/2)*dx;
k4=feval(f,x(k-1)+dx,y(k-1)+k3)*dx;
y(k)=y(k-1)+(k1+2*k2+2*k3+k4)/6;
end
xy=[x;y];
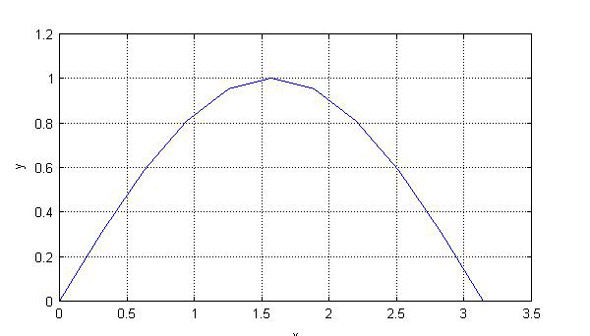
rk4(関数,x初期値,x終端値,分割数,y初期値)と入力すると、変数xyの1行目にx、2行目にyを格納します。例えば、先ほどのdy/dx=cos(x)をxが0からpi、分割数10、yの初期値0で解いてグラフ化するには、コマンドウィンドウで下記のように入力します。すると、図3の結果が得られます。
--> xy=rk4('cos(x)',0,pi,10,0);
--> plot(xy(1,:),xy(2,:));grid('on');
--> xlabel('x');ylabel('y');
実は、MATLABにはodeと呼ばれる微分方程式を数値的に解くコマンド群があり、FreeMatもode45という微分方程式解法のコマンドを持っています。次回はode45の使い方を説明します。
参考文献
- 「MATLABハンドブック」小林一行著、秀和システム刊
- 「はじめてのFreeMat」赤間世紀著、工学社刊
筆者紹介
伊藤孝宏(いとう・たかひろ)
1960年生。小型モーターメーカーのエンジニア。博士(工学)。専門は流体工学、音・振動工学。現在は、LabVIEWを使って、音不良の計測・診断ソフト、特性自動検査装置などの開発を行っている。
Copyright © ITmedia, Inc. All Rights Reserved.